---

Conceptos básicos en geodesia como insumo para un tratamiento adecuado de la información geoespacial

Basic concepts in geodesy as an input for adequate treatment of geospatial information

Jorge Moya-Zamora1

Bepsy Cedeño-Montoya2

Universidad Nacional de Costa Rica, Costa Rica

RESUMEN

La geodesia como la ciencia encargada del estudio de la Tierra incluyendo de manera general su forma, tamaño, campo de gravedad y representación ha necesitado y necesita actualmente de sistemas y marcos de referencia modernos con los cuales se pueda vincular la información, producto de las mediciones realizadas. Se quiere mostrar una serie de conceptos fundamentales en la geodesia, los cuales se relacionan principalmente con el entendimiento de los sistema de referencia, marcos de referencia, datum geodésico, tipos de coordenadas y proyección cartográfica, de forma de establecer sin entrar en amplias deducciones matemáticas, una base general de definiciones que le permitan a los usuarios y profesionales vinculados con las demás geociencias, contar con una referencia de fácil consulta. Se hace además una especial consideración sobre el Sistemas Geocéntrico para las Américas (SIRGAS), su rol e importancia como el proyecto geodésico de mayor impacto técnico en Latinoamérica. Costa Rica cuenta hoy con más de una decena de estaciones GNSS de operación continua debidamente integradas a SIRGAS, cuyas coordenadas geocéntricas constituyen la base geodésica de mayor exactitud con la cuenta el país.

Palabras clave: geodesia; sistema de referencia; marco de referencia; datum; proyección; ITRF2014

ABSTRACT

Geodesy as the science responsible for the study of the Earth including its shape, size, gravity field and representation has needed and currently needs modern systems and frames of reference that can link the information resulting from measurements made. It wants to show a series of fundamental concepts mainly linked with reference systems, reference frames, geodetic datum, types of coordinates and map projection in order to establish, without going into extensive mathematical derivations, a general basis of definitions that allow users and professional linked to other geosciences have a friendly reference. Special consideration on the Sistema Geocéntrico para las Américas (SIRGAS), its role and importance as the geodetic project of greater technical impact on Latinamerica is also done. Today Costa Rica has more than ten continuously operating GNSS stations duly integrated to SIRGAS, whose geocentric coordinates constitute the geodesic basis of greater accuracy of the country.

Keywords: geodesy; reference system; reference frame; datum; projection; ITRF2014

Introducción

Los sistemas de referencia son una necesidad cuando se requiere ubicar objetos. La determinación de la posición debe hacerse teniendo en cuenta una referencia, pero esta referencia, que en principio puede ser arbitraria dependiendo de la finalidad, tiene que ser actualmente considerada de manera global definiendo la posición de los elementos de interés de una forma única. Tradicionalmente las diferentes geociencias han trabajado con sistemas de referencia que se pueden considerar como locales, regionales. Estos sistemas han pasado en las últimas décadas de estar materializados por un conjunto de estaciones pasivas en cada país, a convertirse en sistemas dinámicos definidos por estaciones de medición continua GNSS y otras técnicas de la geodesia espacial. Estas técnicas, acompañadas de modelos matemáticos contemplados dentro procesamiento riguroso de los datos satelitales, permiten que se pueda dar posición a las estaciones terrestres con una exactitud milimétrica. Los marcos de referencia, son por lo tanto, la base para la determinación de una serie de parámetros necesarios para las diferentes aplicaciones como el catastro, la ingeniería, la navegación precisa, los sistemas de información geográfica, la geodinámica y otras aplicaciones de las diferentes geociencias. A nivel global, la Comisión 1 de la Asociación Internacional de Geodesia (IAG) denominada como “Marcos de Referencia”, es la encargada del estudio científico de la problemática para el establecimiento de los marcos de referencia.

1. La forma de la Tierra

La primera aproximación de la verdadera forma de la Tierra es la que asume un sistema esférico, en el cual la ubicación de los puntos sobre su superficie se hace considerando naturalmente un sistema de referencia dado por coordenadas esféricas. El griego Eratóstenes (276 - 195 B.C) realizó la primera determinación del radio de Tierra obteniendo un valor de 6267 Km, solo un 1,6% de diferencia con las mediciones actuales. Siglos después, varias mediciones de arco en diferentes partes del planeta condujeron a la determinación de que la Tierra se aproxima más a una forma elipsoídica, ensanchada en el Ecuador y achatada en los polos.

El geoide representa la verdadera forma de la Tierra. Esta es una superficie equipotencial del campo gravitatorio terrestre (superficie en la cual el valor del potencial gravitatorio es constante) que mejor se adapta al nivel medio del mar (Jekeli, 2006), asumiendo que las diferencias entre las dos superficies son mínimas. La superficie del geoide es irregular debido a las distribución heterogénea de las masas en la Tierra (Lu et al, 2014). Se puede decir que el geoide quiere representar la verdadera forma de la Tierra, haciendo coincidir su superficie con los océanos supuestos en reposo y extendidos por debajo de los contenientes de forma imaginaria (LGFS, 2016).

2. Geodesia

La definición clásica de geodesia dada por Friedrich Robert Helmert en 1880, considera como sus tareas fundamentales la determinación de la forma y representación de la superficie terrestre. En 1878, Heinrich Bruns planteó que el objetivo fundamental de la geodesia es la determinación del potencial gravitatorio. Estas dos definiciones enfocan de una manera global la labor de la geodesia desde el punto de vista geométrico y físico. Hoy día, la geodesia abarca otras tareas de igual importancia permitiendo definir a la geodesia como la disciplina que estudia la medida y representación de la forma de la Tierra y otros planetas, su orientación en el espacio y su campo de gravedad en un espacio tridimensional que varía con el tiempo. La definición de la geodesia ha evolucionado desde la dada a finales del siglo XIX. Torge (2001) dice que “El problema de la geodesia es determinar la figura y campo gravitatorio externo de la Tierra y otros cuerpos celestes como una función del tiempo, por medio de observaciones realizadas dentro y fuera de estos cuerpos”(p.2).

La geodesia abarca disciplinas diversas que pueden agruparse en las siguientes áreas: la geodesia geodinámica vinculada con los estudios tendientes a la descripción cinemática de las placas tectónicas, la geodesia espacial que estudia, entre otros fenómenos, las variaciones en la rotación y orientación de la Tierra, la geodesia física que trabaja con gravimetría en determinación de la figura de la Tierra y la geodesia geométrica o matemática, que involucra los cálculos para obtener posiciones de puntos con una alta exactitud. En el caso de la geodesia espacial, se contempla mediciones de alta precisión realizadas desde, hacia y entre satélites y otros cuerpos celestes para la solución de problemas geodésicos como la determinación de posiciones tridimensionales Tierra con alta exactitud (redes de control), campo de gravedad de la Tierra y las funciones que los describen (geoide) y por último, medición y modelaje de los fenómenos geodinámicos (movimientos del polares, rotación terrestre y deformación de la corteza) (Seeber, 2003). Una definición que integra otra serie de elementos puntuales relacionados con las tareas de la geodesia moderna, es la que se ofrece la Escuela de Ciencias de la Tierra de la Universidad de Ohio State en la dirección: https://earthsciences.osu.edu/divisions/geodetic. Contribuciones de la geodesia a la topografía, el mapeo, la ingeniería, el transporte, a la tecnología espacial, a la investigación científica en geociencias, monitoreo y protección de ambiente, así como en la prevención de desastres naturales puede ser consultado en Lu et al (2014).

Modernamente, todos los aportes de los diferentes tipos de mediciones geodésicas permiten por primera vez, tener datos de alta exactitud destinados a estudiar los cambios del planeta. Es de esta manera como la iniciativa de la IAG denominada como Sistema Global de Observación Geodésica (GGOS), integra en un solo sistema las diferentes técnicas geodésicas, modelos y aproximaciones con el objetivo de lograr a largo plazo, un monitoreo preciso para un mejor entendimiento de la geodinámica y procesos de cambio global (GGOS, 2016).

3. El elipsoide como aproximación de la forma de la Tierra

En geodesia se asume como forma de la Tierra un elipsoide de revolución, el cual es el resultado de hacer girar una elipse alrededor de su eje menor. Este hecho genera una superficie simétrica con respecto al eje polar y el Ecuador. Matemáticamente un elipsoide se puede definir considerando un parámetro para la forma y otro para el tamaño. En la figura 1 se esquematiza un elipsoide de dos ejes.

Figura 1. Elipsoide revolución, el parámetro a es el semieje mayor y el parámetro b es el semieje menor

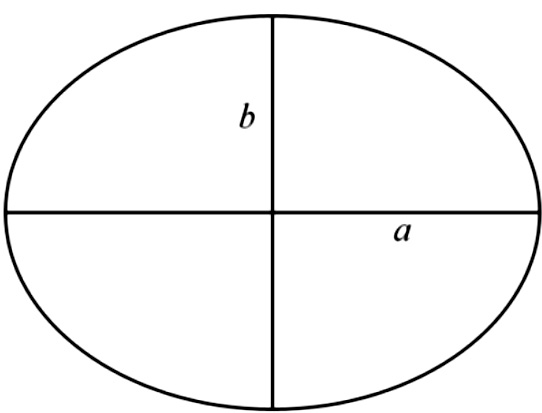
Fuente: Elaboración propia (2017).

Por ejemplo, partiendo de que se conocen los valores de los semiejes a y b, se pueden determinar otras cantidades frecuentemente usadas en los cálculos geodésicos. En el conjunto de ecuaciones (1), f es el achatamiento, e es la primera excentricidad, e’ es la segunda excentricidad y c es el radio de curvatura polar. Es evidente que también se pueden conocer inicialmente a y f así como también se puede partir de los valores de a y f-1.

Al tener el elipsoide doble curvatura, es importante también conocer las relaciones matemáticas que permiten el cálculo del radio de la elipse meridiana M y del radio de curvatura del primer vertical N (ver ecuaciones 2).

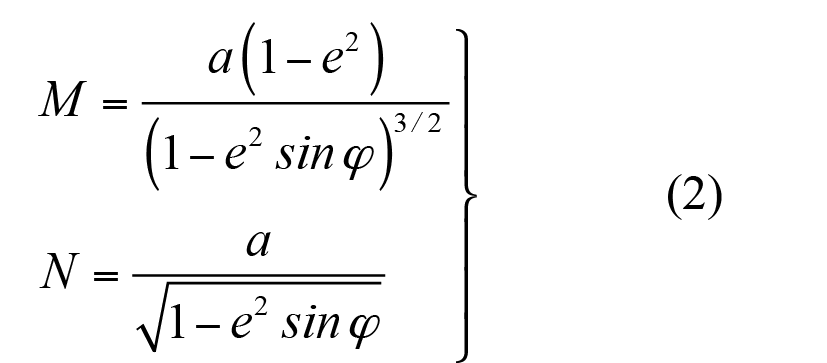
Actualmente y con un incremento notable en la exactitud de los cálculo geodésicos, los elipsoides incluyen, además de sus parámetros geométricos, dos parámetros adicionales: la masa del elipsoide M que representa las propiedades físicas de la Tierra y la velocidad angular de rotación del elipsoide alrededor del semieje menor ω. En el siguiente cuadro, se presentan los principales parámetros geométricos para cuatro de los elipsoides más conocidos y utilizados. Las relaciones matemáticas definen la geometría completa del elipsoide se pueden consultar en (Rapp, 1984), (Jekeli, 2008), (Hooijberg, 1998) y (Hooijberg, 2008).

Cuadro 1. Principales parámetros geométricos para los elipsoide Clarke 1866, Internacional, GRS80 y WGS84

Parámetro	Clarke 1866	Internacional	GRS80	WGS84
a	6378206,4 m	6378388 m	6378137 m	6378137 m
b	6356583,8 m	6356911,946 m	6356752,314 m	6356752,314 m
f	0,003390075304	0,003367003387	0,003352810688	0,003352810672
f-1	294,978698213898	296,999998230593	298,257221538148	298,257222932869
e2	0,006768657997	0,006722670062	0,006694380036	0,006694380004
e’2	0,006814784946	0,006768170238	0,006739496788	0,006739496757

Fuente: Elaboración a partir de Rapp, 1984, Jekeli, 2008, Hooijberg, 1998 y Hooijberg, 2008.

4. Sistemas de coordenadas en geodesia

Es necesario contar con sistemas de coordenadas para ubicar de manera unívoca puntos, líneas y espacios. Si se define un sistema de coordenadas tridimensional con centro en el elipsoide cuyo eje Z coincida con el eje de su rotación, el eje X quede definido por el centro del elipsoide y la intersección del meridiano de referencia sobre el plano de Ecuador y el eje Y perpendicular a los dos anteriores en sentido dextrógiro, se pueden definir dos tipos de coordenadas para cualquier punto. En primer lugar coordenadas cartesianas, que son coordenadas geocéntricas y se denotan como [X, Y, Z] expresadas en metros. Y en segundo lugar, las coordenadas elipsoídicas o geodésicas denominadas como latitud, longitud y altura denotadas por ϕ, λ, h]. La latitud y la longitud elipsoídica son expresadas en grados sexagesimales [°], mientras que la altura elipsoídica se expresa en metros. En la figura 2 se muestra este sistema y los dos tipos de coordenadas para el punto P localizado en la superficie terrestre.

Figura 2. Coordenadas geocéntricas X, Y, Z y coordenadas elipsoídicas ϕ, λ, h

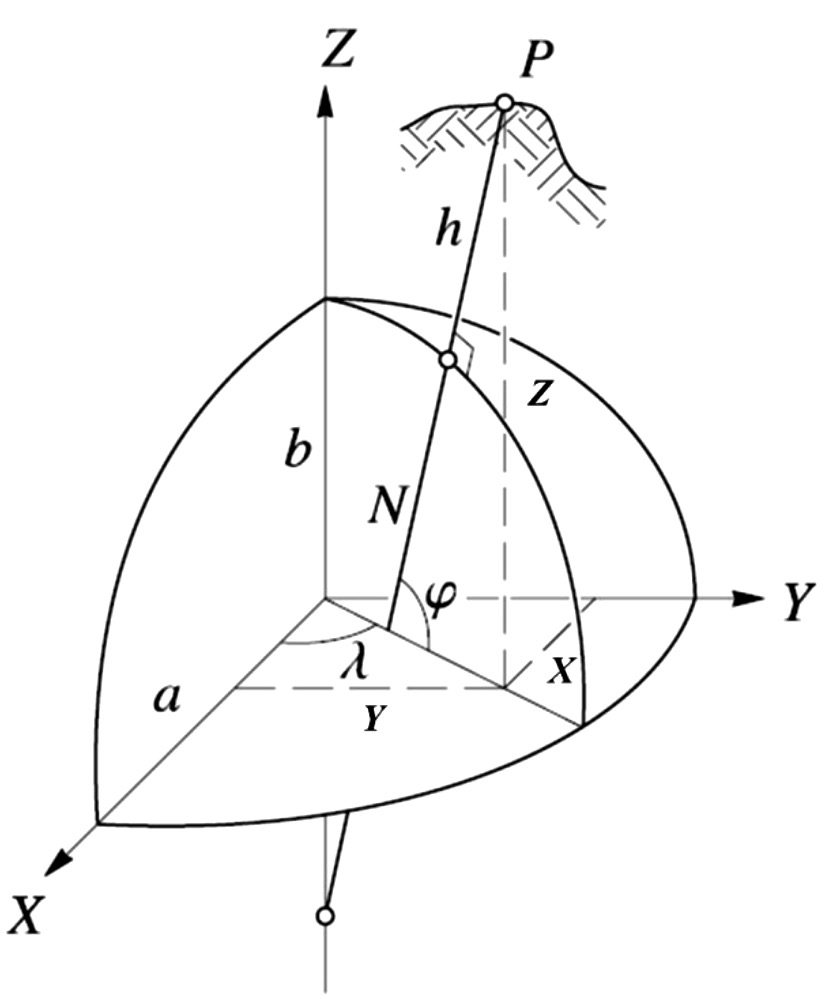
Fuente: Hofmann-Wellenhof et al, 2008, p.278

En el conjunto de ecuaciones (3) se presentan las relaciones que permiten calcular las coordenadas cartesianas [X, Y, Z] a partir de coordenadas elipsoídicas [ϕ, λ, h], mientras que en el conjunto de ecuaciones (4) se tiene el proceso inverso, partiendo de coordenadas cartesianas geocéntricas para obtener coordenadas elipsoídicas. El cálculo de las coordenadas de latitud [ϕ] y altura [h] se realiza de manera iterativa y el mismo se puede consultar en Hofmann-Wellenhof et al (2008), p.281.

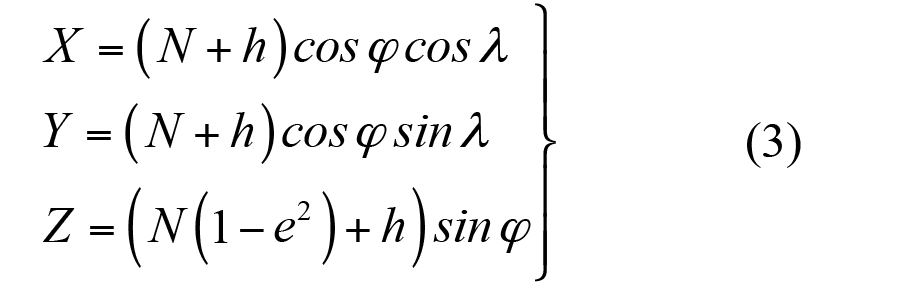
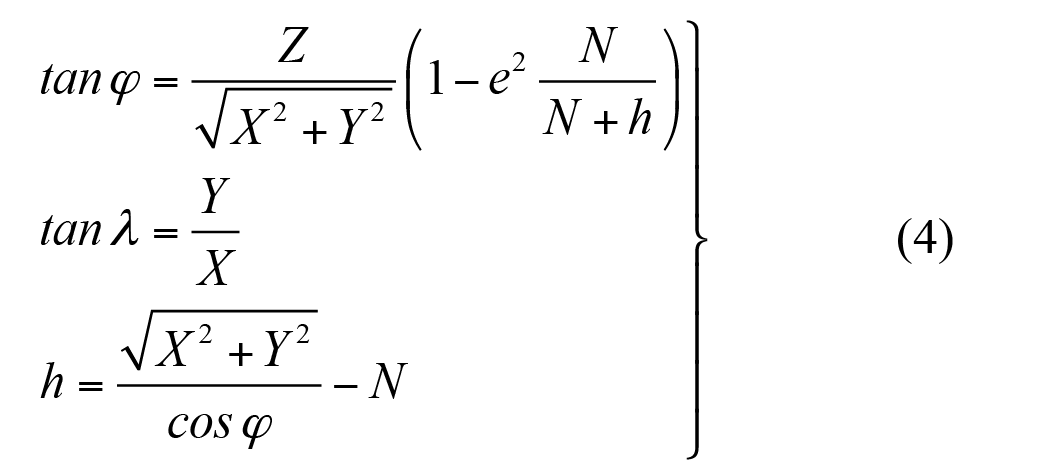
5. Los sistemas geodésicos de referencia

Los sistemas de referencia son necesarios para modelar las observaciones geodésicas como una función de parámetros desconocidos. Los sistemas están definidos en términos de orientación, métrica y curvatura; y en principio son sistemas tridimensionales. La cuarta dimensión, el tiempo, se contempla con base en los movimientos de la Tierra, sus deformaciones y los movimientos de los cuerpos celestes. De la misma forma como se pueden definir sistemas de referencia para la Tierra, se puede hacer por ejemplo para la Luna y el resto de planetas del Sistema Solar. Las observaciones geodésicas y los modelos derivados de ellas necesitan de un aspecto fundamental, que es la definición de unidades básicas de medida. En la geodesia estas unidades son adoptadas del Sistema Internacional (SI) utilizando el metro [m] para la longitud, el kilogramo [Kg] como unidad de masa y el segundo [s] como unidad de tiempo (Torge, 2001). De acuerdo con Drewes (2009), los marcos de referencia geodésicos son necesarios para referir las observaciones geodésicas y poder estimar parámetros en un único sistema global, por lo se deben considerar las siguientes distinciones:

- El sistema de referencia, en el que se definen un conjunto de constantes, convenciones, modelos y parámetros los cuales sirven como una base matemática para la representación de cantidades geométricas y físicas, por ejemplo, un sistema cartesiano tridimensional con origen en el geocentro, orientación ecuatorial, escala métrica y que rote con la Tierra.

- El marco de referencia, el cual es la realización del sistema de referencia y que contempla dos partes: la física, que es la materialización sólida del sistema por medio de un conjunto de puntos, y la matemática, que es la determinación de parámetros, por ejemplo las coordenadas de las estaciones. El acceso a estos puntos se da por medio de ocupaciones o mediciones (Jekeli, 2006).

- El datum geodésico fija de una manera inequívoca la relación entre un marco de referencia y un sistema de referencia por medio de la asignación de un conjunto de parámetros preestablecidos, por ejemplo, las coordenadas del origen del sistema (X0, Y0, Z0), las direcciones de los ejes coordenados X, Y, Z, y la escala o patrón de medida.

Tanto el sistema de referencia, el datum geodésico como el marco de referencia, adicionalmente deben respetar una jerarquía que toma en cuenta los siguientes aspectos (Drewes, 2009):

- La materialización de un sistema de referencia por medio del marco de referencia y la asignación del datum geodésico, no debe cambiar la definición del sistema de referencia.

- La realización del datum debe ser hecha por medio de mediciones independientes del marco de referencia, es decir, los errores de las mediciones o los cambios físicos en las observaciones afectan el marco, pero no el datum.

- La realización matemática del marco de referencia debe ser hecha por medio de algoritmos que mantengan fijos los parámetros del datum y sigan estrictamente los principios definidos en el sistema de referencia.

En los sistemas bidimensionales geodésicos de referencia, el datum se fija por medio de cuatro parámetros: dos que definen el origen, otro para la orientación y otro para la escala. En los modernos sistemas de referencia tridimensionales se fijan siete parámetros para el datum, tres para ubicar el origen del sistema, tres parámetros para la orientación de los ejes coordenados y uno para la escala (Drewes, 2009).

6. Sistema Internacional de Referencia Terrestre (ITRS)

El Sistema Internacional de Referencia Terrestre (ITRS) constituye un conjunto de prescripciones y convenciones junto con el modelado necesario para definir el origen, la escala, la orientación y la evolución en el tiempo de un Sistema de Referencia Terrestre Geocéntrico (GTRS) anteriormente designado como Sistema de Referencia Terrestre Convencional (CTRS). El ITRS es un sistema ideal de referencia, tal como se definió en la resolución Nº 2 de la International Union of Geodesy and Geophysics (IUGG), aprobada en Viena, Austria en 1991 y la resolución Nº2 de la IUGG aprobada en Perugia, Italia en 2007. El ITRS se puede relacionar con el Sistema Internacional de Referencia Celeste (ICRS) mediante el uso de los parámetros de orientación de la Tierra (EOP). El ITRS está definido de acuerdo con las siguientes condiciones (IERS, 2016):

- Es geocéntrico, el centro de masa es definido para toda la Tierra, incluyendo los océanos y la atmósfera.

- La unidad de longitud es el metro en concordancia con el Sistema Internacional y está en correspondencia con las resoluciones de la IAU y la IUGG de 1992 y se obtiene por medio de un apropiado modelado relativista.

- Su orientación está dada inicialmente por el Bureau International de l’Heure (BIH) en 1984.0

- La evolución en el tiempo de la orientación se garantiza mediante el uso de una condición de No-Net-Rotation (NNR) con respecto a los movimientos tectónicos horizontales sobre toda la Tierra.

7. Marco Internacional de Referencia Terrestre (ITRF)

El Marco Internacional Terrestre de Referencia (ITRF) es un conjunto de puntos con coordenadas tridimensionales y velocidades, las cuales hacen la realización del ITRS (IERS, 2016). El grupo de estaciones que determina el ITRF, están equipadas con varios sistemas de medición de la geodesia satelital como Satellite Laser Ranging (SLR), Doppler Orbitography Determination and Radiopositioning Integrated on Satellites (DORIS), Global Navigation Satellite System (GNSS), Very Long Base Interferometry (VLBI) (Altamimi et al, 2002) y (IERS, 2016).

Cada una de estas técnicas contribuye a tener una única solución de ITRF, la cual es determinada por el IERS. El primer ITRF se calculó en 1984 y se denominó BTS84, el cual incluyó en ese momento observaciones del sistema TRANSIT. Desde este primer marco se han calculado diferentes soluciones denominadas como ITRF92, ITRF93, ITRF94, ITRF96, ITRF97, ITRF2000 e ITRF2005, ITRF2008, siendo la más actual el ITRF2014 (IERS, 2016). El ITRF2014 incluye 1499 estaciones localizadas en 975 sitios y cerca del 10% son lugares en donde se tiene 2, 3 o 4 técnicas de medición geodésica tal como se presenta en la figura 3, mientras que la figura 4 se muestra el campo de velocidades resultante asociado al ITRF2014 (IAG, 2016). Las coordenadas geocéntricas de las estaciones, sus variaciones temporales y los parámetros de los EOP están dados a la época de referencia 2010,0 (IERS, 2016)

Figura 3. Localización de las estaciones usadas en la definición del ITRF2014 de acuerdo con la técnica de medición

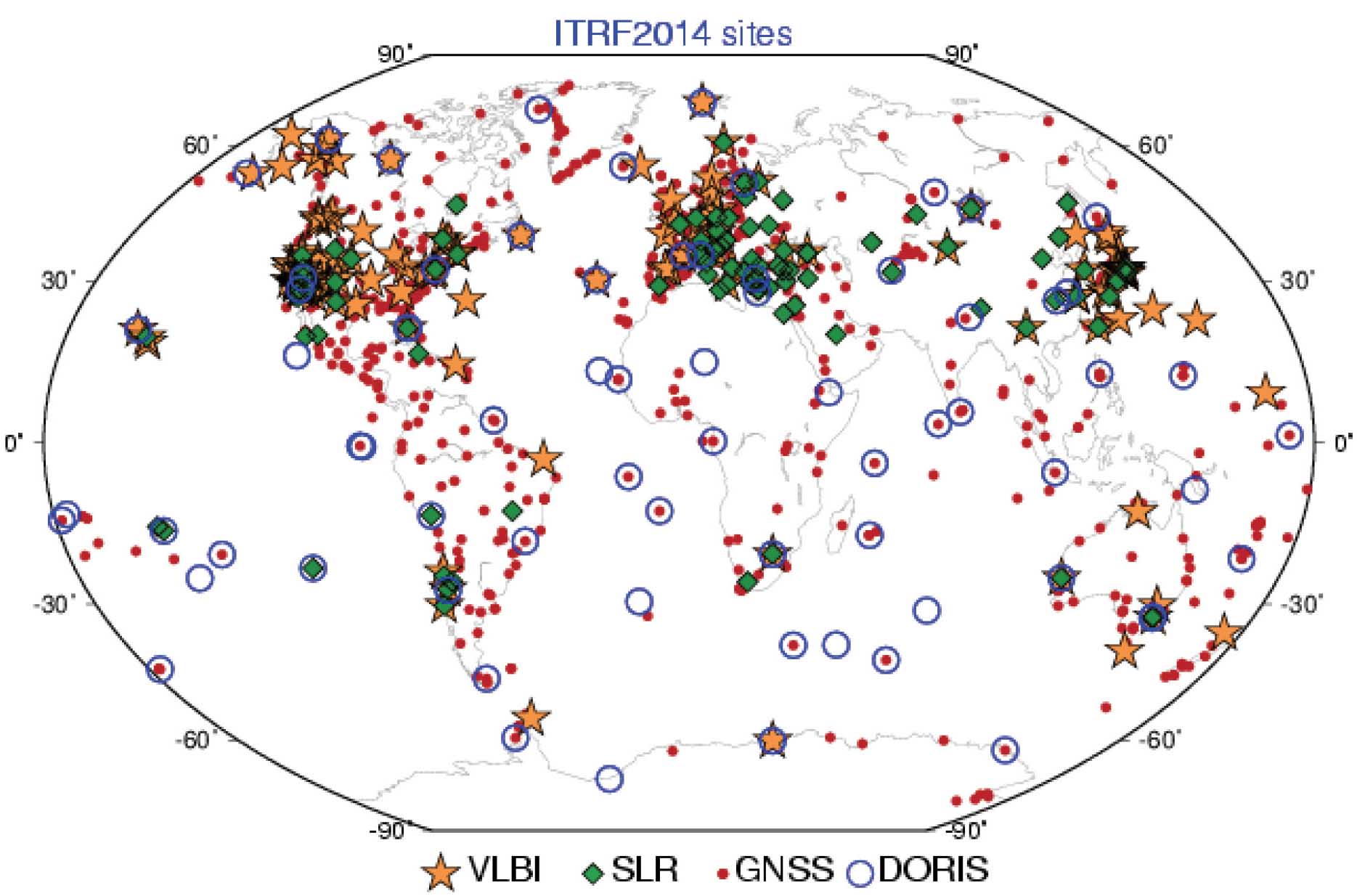
Fuente: http://www.iag-aig.org/

Figura 4. Campo de velocidades horizontal del ITRF2014

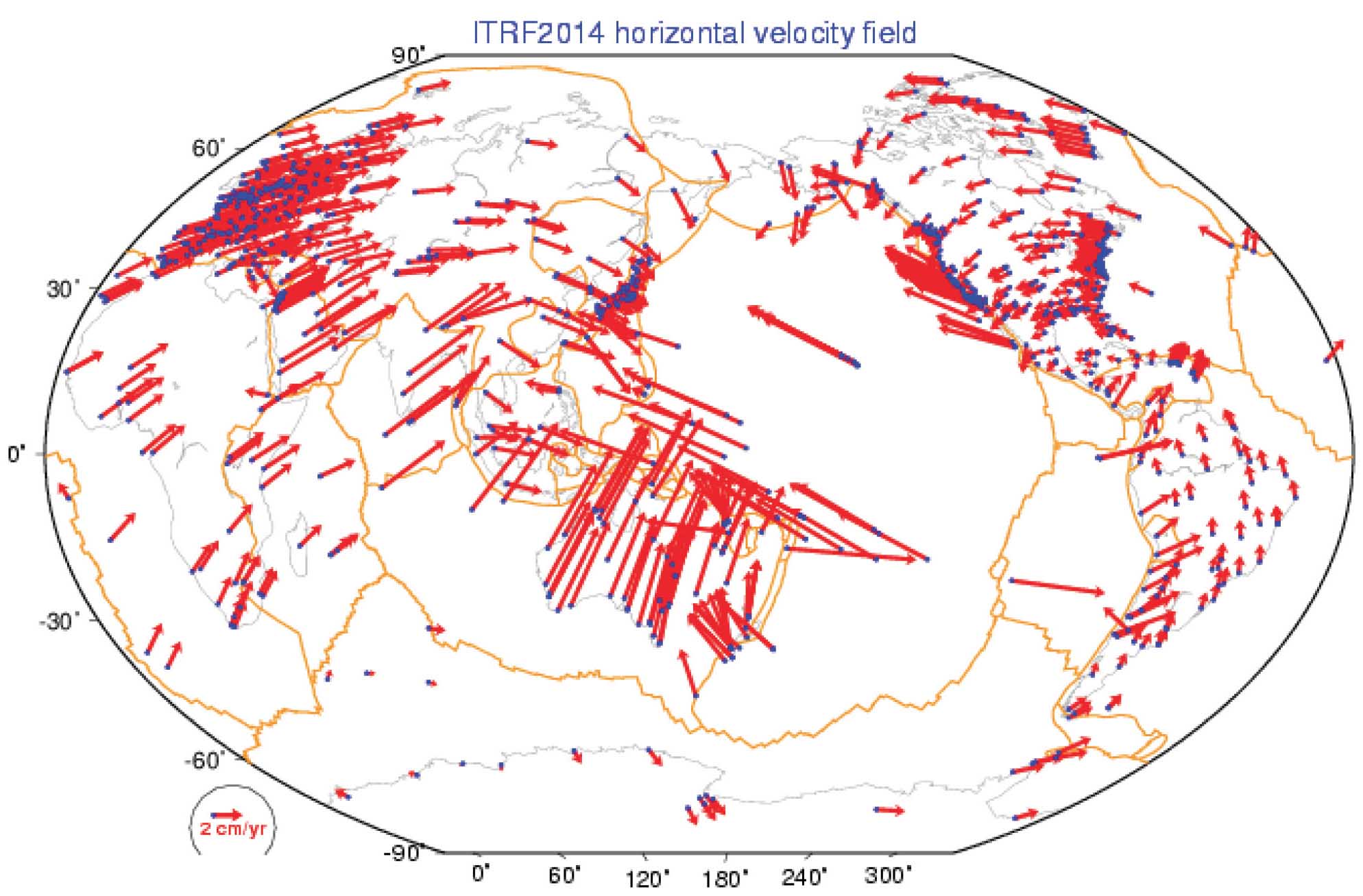
Fuente: http://www.iag-aig.org/

8. El Sistema Geocéntrico para las Américas (SIRGAS)

El proyecto SIRGAS inició formalmente en 1993 bajo el nombre de Sistema Geocéntrico para América del Sur, con el objetivo de materializar el ITRS en Sudamérica (Brunini, 2007) y (Brunini y Sánchez, 2012). En el año 2001, el nombre cambia oficialmente Sistema Geocéntrico para las Américas (SIRGAS), debido fundamentalmente al incremento en el número de estaciones continuas ubicadas en el resto de los países del continente. Las actividades científicas y técnicas son coordinadas por los Grupos de Trabajo en colaboración con el consejo científico y los representantes de la IAG y el IPGH (SIRGAS, 2016).

La definición de SIRGAS es idéntica al ITRS y su realización es una densificación del ITRF, ocupándose además de la parte vertical. La realización de SIRGAS es la densificación regional del marco global de referencia terrestre ITRF en América Latina y El Caribe. Las coordenadas SIRGAS están asociadas a una época específica de referencia y su variación con el tiempo es tomada en cuenta ya sea por las velocidades individuales de las estaciones SIRGAS o mediante un modelo continuo de velocidades que cubre todo el continente. Las realizaciones o densificaciones de SIRGAS asociadas a diferentes épocas y referidas a diferentes soluciones del ITRF, materializan el mismo sistema de referencia, y sus coordenadas, reducidas a la misma época y al mismo marco de referencia (ITRF), son compatibles en el nivel milimétrico. La extensión del marco de referencia SIRGAS está dada a través de densificaciones nacionales, las cuales a su vez sirven de marcos de referencia local (Brunini et al, 2012) y (SIRGAS, 2016).

Las estaciones GNSS de operación continua que están integradas de manera oficial a SIRGAS sobrepasan las 400 en todo el continente americano, de las cuales 59 son estaciones del Servicio Internacional del GNSS (IGS). Esta red de funcionamiento continuo denominada como SIRGAS-CON y semanalmente es calculada y sus coordenadas a la época de observación, están en el mismo sistema que las órbitas satelitales finales GNSS (SIRGAS, 2016). En la figura 5 se muestra la red SIRGAS-CON a junio de 2016.

Figura 5. Red de estaciones de operación continua GNSS para SIRGAS a junio de 2016

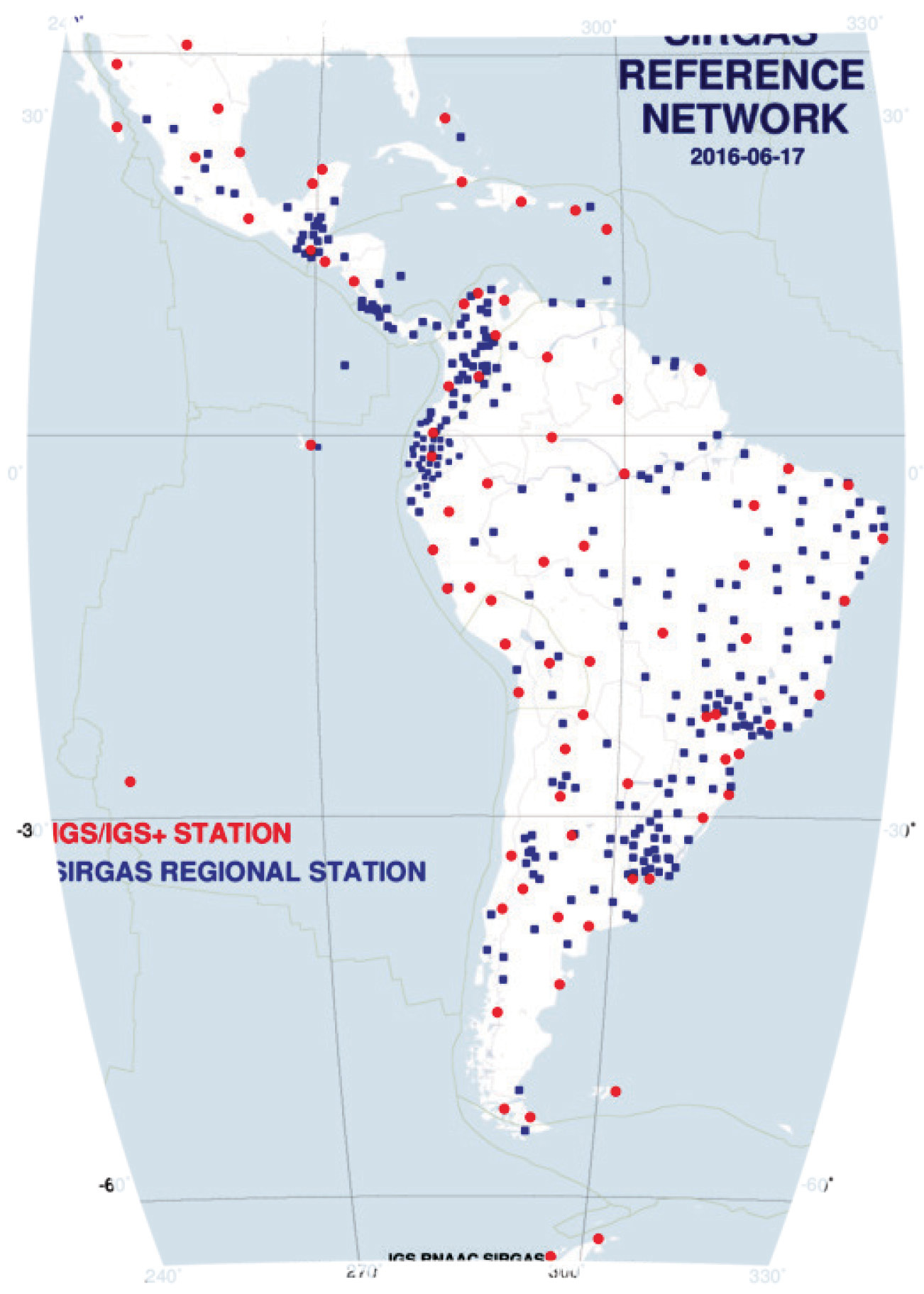
Fuente: http://www.sirgas.org

Todos los productos que se generan como parte de los diferentes proyectos de investigación enmarcados en SIRGAS son de acceso público y gratuito. Entre ellos, uno de los más representativos son las coordenadas semanales de las estaciones de la red SIRGAS-CON. Este conjunto de coordenadas se calcula en una primera etapa por los diferentes Centros de Procesamiento SIRGAS ubicados en Argentina, Brasil, Chile, Colombia, Costa Rica, Ecuador, México, Uruguay y Venezuela, los cuales, entre otras tareas, están encargados de adelantar el procesamiento semanal de la totalidad de la red SIRGAS-CON.

Los datos generados (soluciones semilibres) por cada uno de los Centro de Procesamiento, son enviados semanalmente a los dos Centros de Combinación SIRGAS, localizados en el Instituto Brasileiro de Geografía y Estadística (IBGE) de Brasil y el Instituto Alemán de Investigaciones Geodésicas de la Universidad Técnica de Múnich (DGFI) en Alemania en donde se encargan de generar la solución final semanal de la red SIRGAS-CON. Las coordenadas geocéntricas que resultan de este proceso están vinculadas al ITRF considerado a la época de la medición. Para mayores detalles sobre el proceso de cálculo de la red SIRGAS-CON se puede consultar la dirección: http://www.sirgas.org/

8.1. La red de estaciones SIRGAS de Costa Rica

En la actualidad Costa Rica cuenta con un total de 14 estaciones GNSS de operación continua integradas oficialmente a la red SIRGAS-CON. En el cuadro 2 se presentan el nombre de cada una de las estaciones y la institución nacional administradora, mientras que en la figura 4 se muestra su ubicación. En esta figura, el cuadro de color negro se detalla en el extremo inferior mostrando la localización de las 4 estaciones ubicadas en la parte central del país, mientras que las restantes estaciones se indican por círculos de color rojo. La estación ETCG fue la primera en ser oficialmente incluida en el año 2003, mientras que la estación VUKE ha sido la última en ser vinculada a esta red. De la totalidad de estaciones, UCRI se encuentra temporalmente deshabilitada, y la estación NICY ha sido excluida del procesamiento hasta que sea reinstalada en otra ubicación.

Cuadro 2. Nombre de las estaciones GNSS integradas a la red SIRGAS-CON y la institución administradora

Estación	Administrador	Lugar
AACR	Instituto Costarricense de Acueductos y Alcantarillados	Pavas, San José
CIQE	Instituto Geográfico Nacional de Costa Rica	Ciudad Quesada, Alajuela
CRLP	Laboratorio PRIAS. Centro Nacional de Alta Tecnología	Rohrmoser, San José
ETCG	Centro Nacional de Procesamiento de Datos GNSS. Universidad Nacional	San Pablo, Heredia
ISCO	UNAVCO	Isla del Coco, Puntarenas
LIBE	Instituto Geográfico Nacional de Costa Rica	Liberia, Guanacaste
LIMN	Instituto Geográfico Nacional de Costa Rica	Limón, Limón
NICY	Instituto Geográfico Nacional de Costa Rica	Nicoya, Guanacaste
NEIL	Instituto Geográfico Nacional de Costa Rica	Ciudad Neily, San José
PUNT	Instituto Geográfico Nacional de Costa Rica	Puntarenas, Puntarenas
RIDC	Instituto Geográfico Nacional de Costa Rica	Curridabat, San José
SAGE	Instituto Geográfico Nacional de Costa Rica	San Isidro del General, San José
UCRI	Escuela de Ingeniería Topográfica. Universidad de Costa Rica	San Pedro, San José
VUKE	Instituto Costarricense de Acueductos y Alcantarillados	Orosi, Cartago

Fuente: Elaboración propia (2017).

Figura 6. Ubicación de las estaciones GNSS de Costa Rica integradas a la red SIRGAS-CON

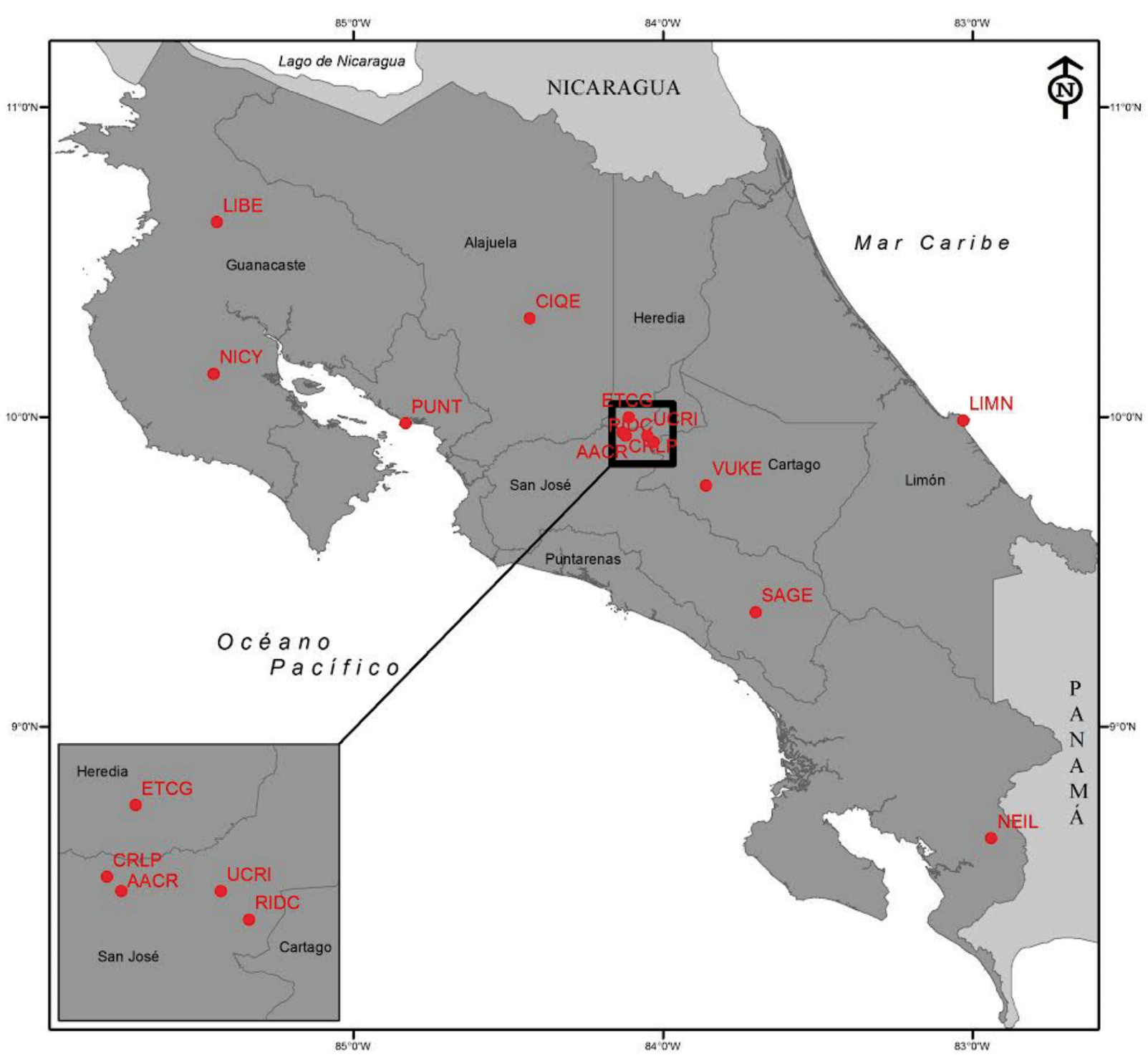
Fuente: Elaboración propia

La red de estaciones SIRGAS de Costa Rica que se encuentran activas, constituyen hoy en día la mejor y la más actualizada referencia geodésica con la cuenta el país, ya que sus datos se procesan semanalmente bajo estrictos estándares y sus coordenadas geocéntricas se vinculan al ITRF más actualizado. Las coordenadas semanales finales se pueden descargar libremente de la web de SIRGAS en la dirección: http://www.sirgas.org/index.php?id=153.

9. Transformación de coordenadas entre sistemas tridimensionales

Dos sistemas cartesianos geocéntricos tridimensionales se pueden relacionar por medio de las coordenadas conocidas de un conjunto de puntos en ambos sistemas. El modelo inicial es conocido como transformación semejante de Helmert, es decir no produce deformaciones en los campos puntuales que se están relacionando. En la figura 7 se representa el esquema general de la transformación espacial de coordenadas, en donde se tiene un sistema cartesiano A y un sistema cartesiano B. El punto P posee coordenadas geocéntricas tanto en el sistema A [XA, YA, ZA] como en el sistema B [XB, YB, ZB]. De esta manera, los dos sistemas se relacionan por medio de 7 parámetros que corresponden con un vector T de tres traslaciones (ΔX, ΔY, ΔZ) entre los orígenes de ambos sistemas, una matriz de rotación R que reúne los giros alrededor de los ejes X, Y, Z respectivamente y denominados como RZ, RY, RX y un factor de escala m.

Figura 7. Esquema de la transformación tridimensional de coordenadas

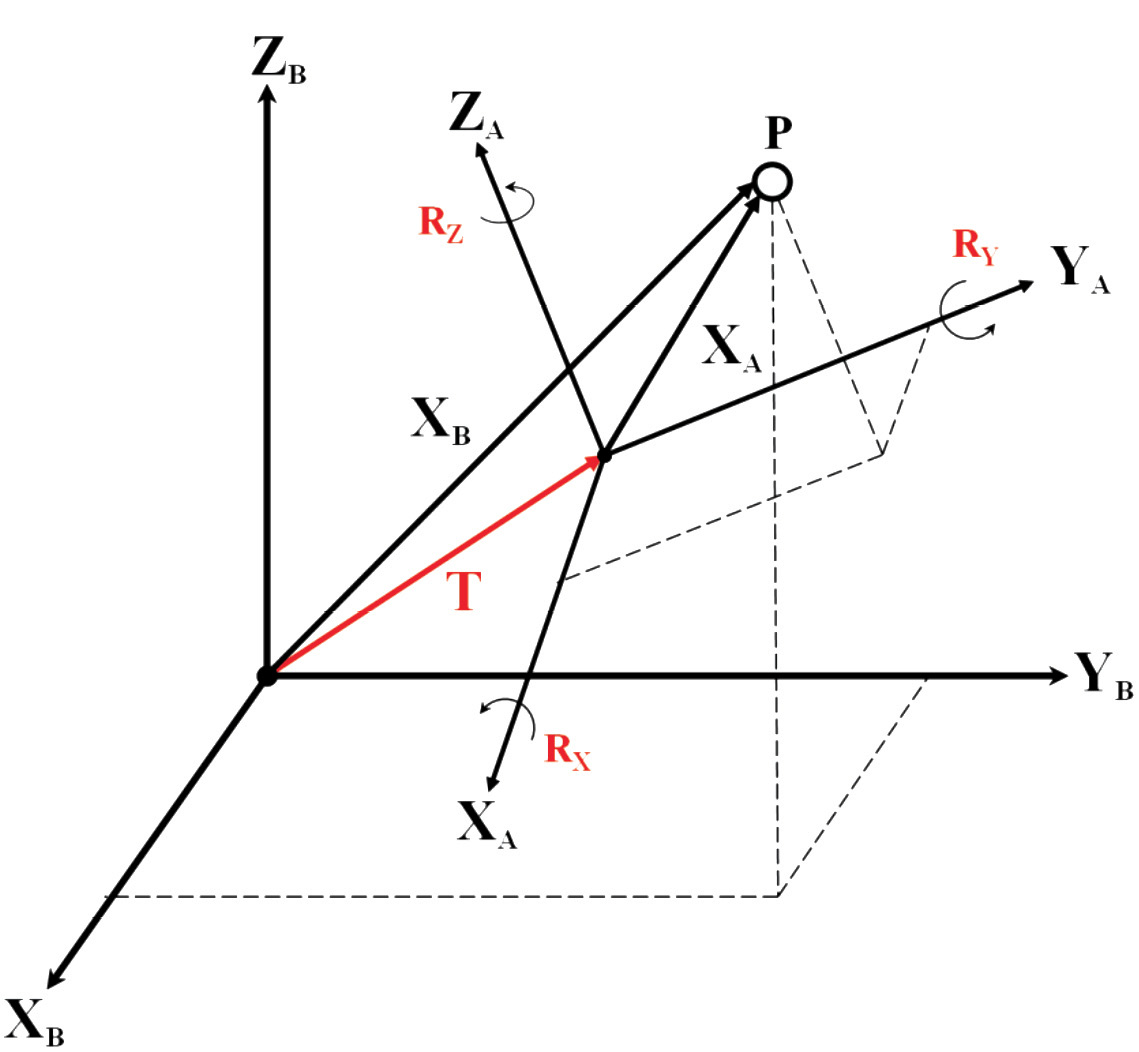
Fuente: Adaptado de Hoffmann-Wellenhof et al, 2008, p. 277

El modelo es conocido como Bursa-Wolf, derivados de los trabajos de Bursa (1962) y Wolf (1963) y en la ecuación (5) se presenta la relación general que permite transformar las coordenadas del sistema A al sistema B, mientras que la ecuación (6) representa el planteamiento matricial. En el caso de las rotaciones se consideran ángulos relativamente pequeños y en unidades de radianes por lo que el coseno de éstos ángulos es prácticamente unitario y el seno del ángulo es igual al ángulo (Deakin, 2006) y (Hoffmann-Wellenhof et al, 2008).

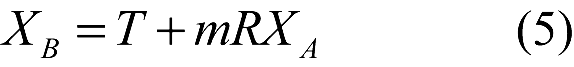
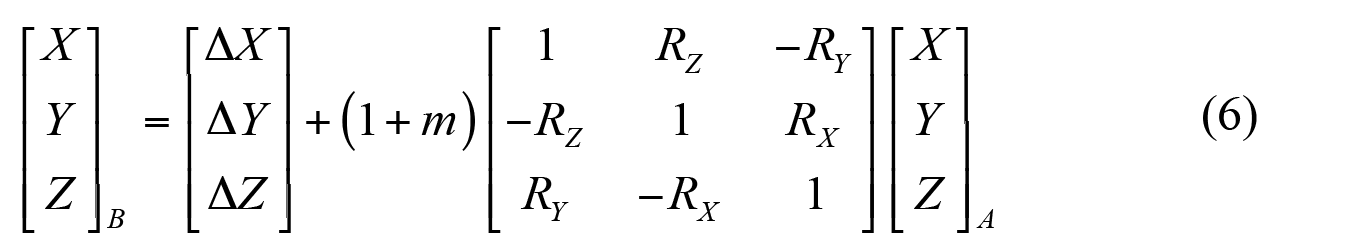
Si el modelo de transformación considera como origen para las rotaciones el centro de gravedad del sistema A, la ecuación (6) se amplía incluyendo estas coordenadas [X0, Y0, Z0] tal como se muestra en el conjunto de ecuaciones (7) llegando al modelo conocido como Molodensky-Badekas (Deakin, 2006) derivado de los trabajos de Molodensky (1962) y Badekas (1969).

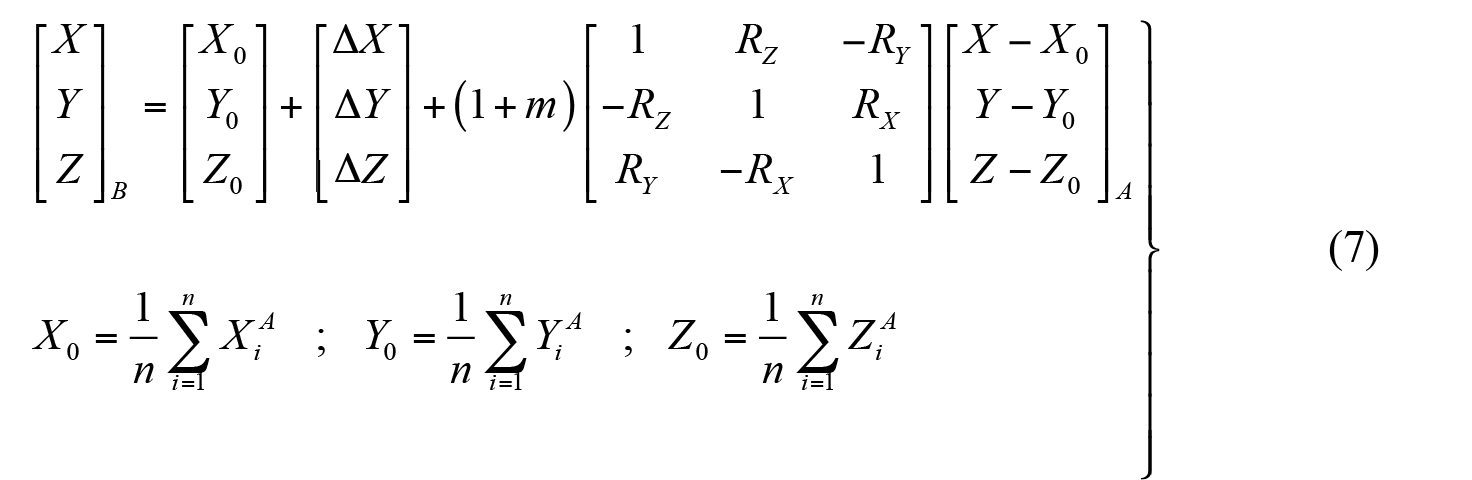
Para una transformación de datum se parte de los dos vectores de coordenadas geocéntricas referidos a los sistemas que se quiere relacionar, por ejemplo poder transformar coordenadas referidas a un datum convencional a coordenadas en un datum satelitario. Por lo tanto, las ecuaciones de transformación deben plantearse de forma de determinar los 7 parámetros de transformación a partir de los valores de las coordenadas de los puntos idénticos. Este proceso se realiza aplicando el algoritmo de ajuste geodésico por mínimos cuadrados con f=3p-u grados de libertad, donde p es el número de puntos idénticos (se requieren al menos de tres puntos) y u es la cantidad de parámetros a calcular o incógnitas.

En el caso de transformaciones entre sistemas cuyas coordenadas se deriven de mediciones satelitales GPS o GNSS, el valor de u se reduce a 6 ya que el parámetro de la escala en ambos sistemas es el mismo. Los parámetros de transformación resultantes están expresados en unidades de metros para las tres traslaciones, unidades de radianes para los tres ángulos de rotación y partes por millón [ppm] para la escala.

10. Coordenadas verticales

La ubicación de un punto en la superficie terrestre en el cual se han realizado mediciones con sistemas de posicionamiento satelital estará dada primariamente por sus coordenadas cartesianas geocéntricas [X, Y, Z] o sus correspondientes coordenadas elipsoídicas [ϕ, λ, h]. La altura elipsoídica es la distancia de un punto en la superficie terrestre al elipsoide considerado medida sobre la perpendicular al elipsoide. Sin embargo, en la gran mayoría de aplicaciones prácticas que requieren de la coordenada vertical, se usa el geoide como superficie de referencia. Este tipo de alturas físicas son el resultado procesos convencionales de medición, en los cuales el instrumento se orienta según la dirección de la gravedad, con su eje vertical coincidiendo con la llamada línea de la plomada y su plano horizontal es tangente a la superficie equipotencial respectiva.

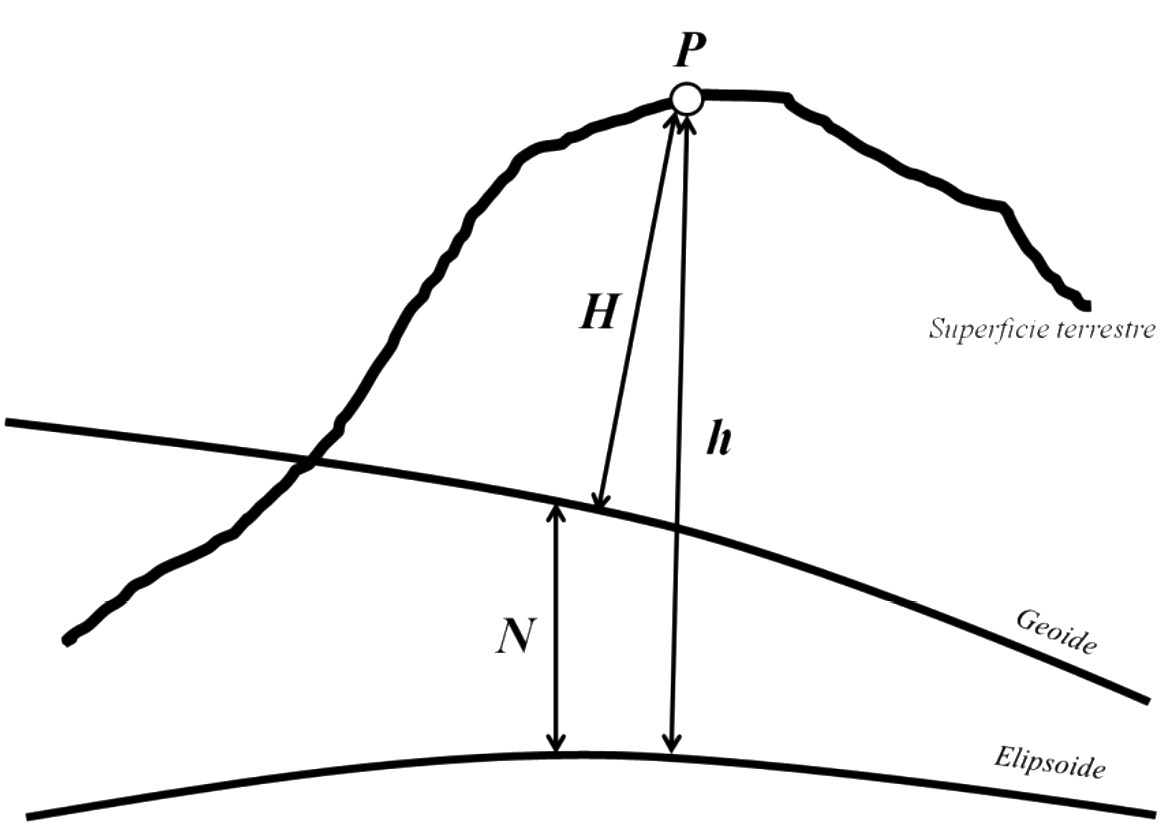
En la figura 8 el punto P ubicado en la superficie terrestre tiene dos coordenadas verticales, la altura elipsoídica [h] que es geométrica y la altura física [H] que es la distancia desde el punto P hasta la normal en la superficie del geoide medida sobre la línea de la plomada. La relación entre el elipsoide y el geoide estará dada por medio de la ondulación del geoide [N], que es la distancia que se separa el geoide del elipsoide. Si los procesos de nivelación son acompañados de mediciones de gravedad y se efectúa el adecuado procesamiento de los mismos, se podrá obtener el denominado número geopotencial [C] dado por las diferencias de potencial entre los puntos nivelados. La denominada cota de un punto, es por lo tanto, el cociente entre el valor de número geopotencial y el valor de la gravedad media [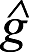]. Si la superficie de referencia para las alturas físicas es el geoide, se tendrán en consecuencia alturas ortométricas.

Figura 6. Relación entre la altura física referida al geoide, la altura elipsoídica referida al elipsoide y la ondulación del geoide

Fuente: Elaboración propia

Si sobre dos puntos A y B se conocen tanto las alturas elipsoídicas hA y hB y además se han realizado mediciones convencionales de nivelación y gravedad permitiendo conocer las correspondientes alturas ortométricas HA y HB, la relación con la ondulación del geoide estará dada por la ecuación (8).

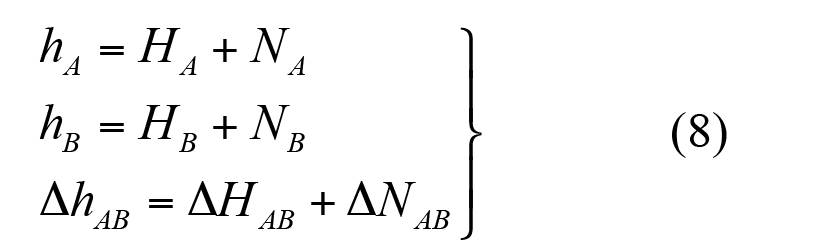
Es importante recalcar que obtener alturas físicas a partir de alturas elipsoídicas y modelos de ondulación del geoide no se satisface plenamente la última relación de conjunto de ecuaciones (8) debido entre otras causas, a la diferente exactitud de las alturas elipsoídicas y las alturas físicas. En las primeras se tienen valores de orden centimétrico y en las segundas, exactitudes milimétrica relativas. Para aplicaciones en las que se requiera una exactitud de varios decímetros a un par de metros, una alternativa es utilizar la última relación de la ecuación (8). Los conceptos teóricos y desarrollos matemáticos completos sobre este tema se pueden consultar en Moritz en (1979), Heiskanen y Moritz en (1985), Torge en (1989) y Hofmann-Wellenhof y Moritz en (2006).

11. Proyecciones cartográficas

En los apartados anteriores es evidente que cualquier punto sobre la superficie terrestre será ubicado por medio de una terna de coordenadas geocéntricas y sus respectivas coordenadas elipsoídicas. Sin embargo, considerando que una de las tareas fundamentales de la geodesia es la representación de los elementos terrestres se necesitará para este fin, trabajar solamente con las coordenadas elipsoídicas de latitud y longitud.

Las proyecciones cartográficas son funciones matemáticas que permiten obtener coordenadas planas a partir de coordenadas elipsoídicas. La forma general está dada en el conjunto de ecuaciones (9), donde x’, y’ representan las coordenadas planas o cartográficas de un punto, F1 y F2 son las funciones de proyección que tienen implícitas las propiedades de equidistancia, equivalencia o conformidad (Bretterbauer, 2002).

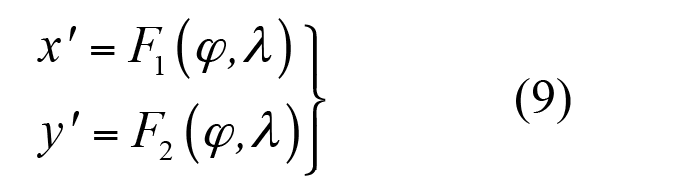
Las aplicaciones geodésicas implican generar mapas conformes, entiendo la conformidad como aquellas propiedades matemáticas en las funciones de proyección, que preservan o mantienen los ángulos en lo diferencial, es decir, si el valor de un ángulo sobre el elipsoide deberá ser igual inclusive después de ser proyectado a la carta.

La meta de las proyecciones cartográficas es proyectar la superficie del elipsoide o superficie original a la carta o superficie imagen, la cual no puede darse sin sufrir deformaciones pues se está pasando de una superficie curva a una plana. Convencionalmente, se entiende que la información de partida debe ser trasladada primeramente superficie denominada como auxiliar, cuya característica principal es que sean desarrollables en un plano. Al respecto se distinguen los siguientes casos:

- Proyección cónica: se entiende como un cono que rodea la superficie del elipsoide el cual es tangente en un paralelo específico llamado de paralelo de contacto o estándar. Esto implica que el cono sea de sección elíptica y las funciones de proyección generan un haz de rectas para los meridianos y círculos concéntricos para los paralelos. Tanto los meridianos como los paralelos parten de un punto llamado vértice del cono. Generalmente, se define que el paralelo de contacto se proyecte sin distorsión. La proyección de Lambert es el ejemplo clásico de una proyección cónica conforme.

- Proyección cilíndrica: Si el punto denominado como vértice del cono se extiende hacia el infinito, el cono se convierte en un cilindro que será tangente en el Ecuador e igualmente de sección elíptica. En posición transversa, el cilindro es tangente a un meridiano que se denominada meridiano de contacto o estándar, el cual se proyectará sin distorsión en el mapa.

- Proyección azimutal: Si por el contario, el punto vértice del cono se hace coincidir con uno de los polos, el cono se convierte en un plano tangente precisamente a uno de los polos. Este tipo de proyección es usada evidentemente para las zonas polares, donde los meridianos son un haz de rectas que parten del punto de tangencia, mientras que los paralelos son círculos concéntricos con centro en el punto de tangencia. Dependiendo de las características que se necesiten, por ejemplo las funciones de proyección pueden generar meridianos sin distorsión.

12. Transformación polinómica

Este método consiste fundamentalmente en la determinación de los coeficientes de un polinomio de grado n, el cual representa la superficie de mejor ajuste entre los dos campos puntuales. El modelo clásico utilizado se plantea inicialmente en términos de correcciones a las coordenadas geodésicas (NIMA, 2004). El modelo es conocido también como regresión múltiple y la determinación de los coeficientes del polinomio se hace por medio de un ajuste por mínimos cuadrados considerando las coordenadas de los puntos idénticos.

En la ecuación (10) se presenta una adaptación de la función original para los casos en que se requiera realizar una transformación entre coordenadas de distintos planos cartográficos, en donde NB, EB son las coordenadas en el plano cartográfico B, a00 y b00 son términos constantes, aij, bij son los coeficientes del polinomio y n, e son las coordenadas reducidas a los respectivos baricentros. En este caso se quiere obtener coordenadas en el plano B a partir de los coeficientes de los dos polinomios y de las coordenadas reducidas del plano A.

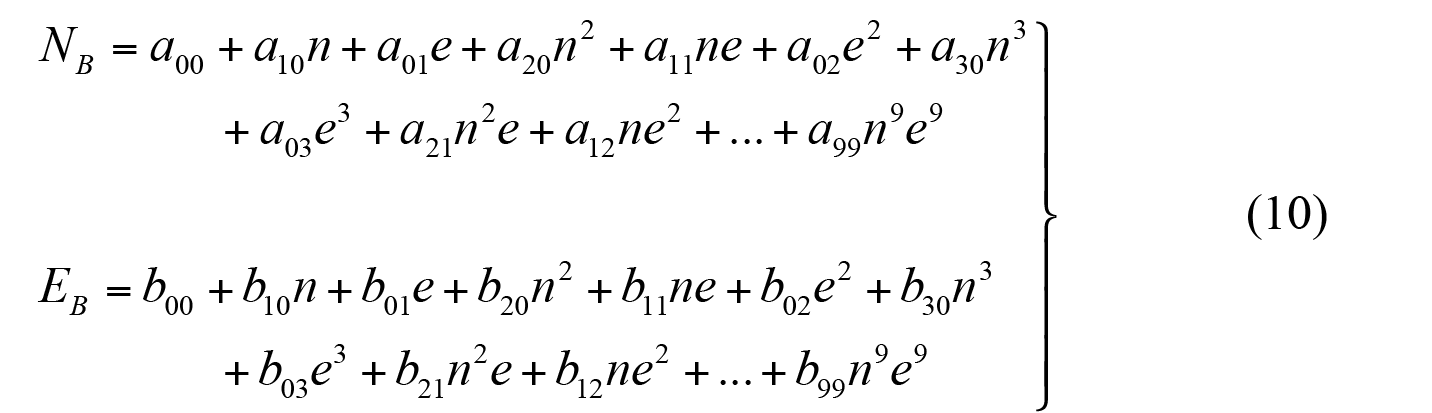
En este tipo de transformación, el polinomio se ajustará mejor a los puntos implicando por lo tanto una afinidad entre los dos campos puntuales. No debe entenderse lo anterior como una mejoría en la transformación al elevar el grado de polinomio, ya que como en cualquier proceso de este tipo la exactitud de los resultados dependerá de la calidad y la distribución de los puntos idénticos.

Conclusiones

- Es de suma importancia, para los usuarios que trabajen con información geoespacial, tener un conocimiento general sobre la base teórica de los fundamentos de la geodesia, como la ciencia encargada del estudio del sistema Tierra. Se han expuesto de manera general una serie de conceptos necesarios que facilitarán esta tarea, siendo necesario que el usuario profundice mucho más en los temas que le demanden un interés particular.

- La determinación precisa de la forma de la Tierra ha sido y sigue siendo una de las tareas fundamentales de la geodesia. Desde esa perspectiva se debe tener claro que dependiendo de las aplicaciones que se requieran, es suficiente considerar un modelo simplificado de la Tierra, es decir una esfera, sin embargo, las finalidades de carácter oficial implican necesariamente adoptar un modelo más complejo como el elipsoide de revolución como la mejor aproximación a la forma real de la Tierra.

- El usuario debe tener presente que la información geoespacial no está aislada, debe estar generada dentro de una estructura matemática diseñada con propósitos muy claros. De ahí que es importante tener presente los conceptos generales de sistema de referencia como la idealización matemática, el de marco de referencia como la materialización en el terreno del sistema de referencia y de la misma forma el concepto de datum, el cual está vinculado con una serie de parámetros que permiten la relación directa entre el sistema y el marco de referencia. Por supuesto, no debe haber mezcla de los conceptos anteriores con el elipsoide que en muchas aplicaciones y productos es erróneamente entendido como un datum. Es importante dejar claro que cada uno tiene sus características y no deben usarse de manera indistinta.

- Es claro como las diferentes técnicas, algoritmos y modelos matemáticos permiten trabajar actualmente con marcos de referencia dinámicos. El ITRF2014, constituye la mejor referencia global, pues se ha determinado con series de datos muy largas y contemplando los cambios en las estaciones de referencia.

- Los sistemas de coordenadas son básicos cuando se trabaja con información geoespacial. Es imperativo conocer que modernamente la información puede estar descrita ya sea en coordenadas geocéntricas (resultados de SIRGAS), coordenadas geodésicas o elipsoídicas (resultados de levantamientos GNSS) o coordenadas cartográficas y de ahí la importancia de saber cómo están relacionadas. En la parte vertical, se expusieron brevemente dos conceptos fundamentales, el de altura geométrica o elipsoídica y el de altura física. Ambos están vinculados por la ondulación del geoide, sin embargo, se recomienda ampliamente informarse adecuadamente cuando las necesidades requieran el uso de esta componente.

- La relación entre dos diferentes datum está dada por medio de los modelos descritos en el apartado 9, los cuales son semejantes. La determinación de los parámetros de transformación entre dos datum parte de un conjunto de puntos idénticos, es decir de puntos con coordenadas geocéntricas conocidas en ambos sistemas. Los parámetros de transformación serán tan buenos como lo sean las coordenadas de partida y la distribución espacial de los puntos. Se debe hacer notar que la aplicación de un conjunto de parámetros de transformación, no mejorará las coordenadas del campo resultante.

- En el apartado 12 se presentó el modelo clásico de transformación polinómica en su adaptación a dos planos cartográficos diferentes. Este tipo de transformación es afín y la misma se suele utilizar ante la ausencia de las variables geodésicas respectivas, que permitan la aplicación de una transformación de 7 parámetros entre sistemas cartesianos geocéntricos. Lo anterior implica que una transformación de este tipo (polinómica) es una solución aceptable desde el punto de vista cartográfico. Existen otras variantes de modelos de transformación que el lector puede consultar en la bibliografía respectiva.

- Las relaciones matemáticas que permiten la conversión y la transformación de coordenadas geodésicas y de coordenadas cartográficas, la georreferencia y la ortorectificación, están integradas en las herramientas de los SIG. Sin embargo, el resultado de cada proceso dependerá principalmente de los insumos aportados por el usuario, especialmente en cuanto a la referencia de los datos.

- Finalmente, se presentaron generalidades sobre el Sistema de Referencia Geocéntrico para las Américas (SIRGAS) cuya influencia en Latinoamérica ha sido muy importante. En Costa Rica se cuenta con más de una decena de estaciones GNSS de operación continua que materializan el ITRF en el país. Además, esta red representa actualmente la referencia geodésica de más alta calidad y con la mejor exactitud.

Referencias

Altamimi, Z., P. Sillard y C. Boucher. (2002). ITRF2000: A New release of the International Terrestrial Reference Frame for Earth Science Applications. Journal of Geophysical Research, 107(B10), 214. 1-19.

Badekas, J. (1969). Investigations related to the establishment of a world geodetic system. Report No. 124, Department of Geodetic Science, Ohio State University, Columbus, Ohio.

Bursa, M. (1962). The theory for the determination of the non-parallelism of the minor axis of the reference ellipsoid and the inertial polar axis of the earth, and the planes of the initial astronomic and geodetic meridians from observations of artificial earth satellite. Studia Geophysica et Geodetica, 6, 209-214.

Bretterbauer, K. (2002). Die runde Erde eben dargestellt Abbildungslehre und sphärische Kartennetzentwürfe. Instituto de Geodesia y Geofísica. Departamento de Geodesia Avanzada. Universidad Técnica de Viena, Austria. 106 pp.

Brunini, C. (2007). SIRGAS: Sistema de Referencia Geocéntrico para las Américas. La Plata, Argentina Simposio “IDE América: Conceptos, Prácticas y Proyectos” IPGH-IGAC, Bogotá.

Brunini, C. y Sánchez, L. (June, 2012). Geodetic activities in Latin America and The Caribbean: always IN. Coordinates, VIII, (6), 14-21.

Bruns, H. (1878). Die figure des Erde. Berlin: Editorial P. Stankiewicz,

Drewes, H. (Ed). (2009). Geodetic Reference Frames. International Association of Geodesy Symposium 134. Springer-Verlag Berlin Heidelberg. DOI 10.1007/978-3-642-00860-3_39

Deakin, R. (2006). A Note on the Bursa-Wolf and Molodensky-Badekas Transformations. School of Mathematical & Geospatial Sciences. RMIT University, Australia. En línea. Disponible en https://www.researchgate.net/publication/

GGOS. (2016). Global Geodetic Observing System. En línea. Disponible en: http://www.ggos.org/

Heiskanen, W. y Moritz, H. (1985). Geodesia Física. Instituto Geográfico Nacional de España, Instituto de Astronomía y Geodesia. Madrid, España. 371 pp.

Hoffmann-Weelenhof, B., Lichtenegger, H. y Wasle, E. (2008). GNSS Global Navigation Satellite Systems GPS, GLONASS, Galileo & more. Springer Wein, New York. Estados Unidos. 568 pp.

Hooijberg, M. (1998). Practical Geodesy Using Computer. Springer-Verlag Berlin, Alemania. 308 pp.

Hooijberg, M. (2008). Geometrical Geodesy Using Information and Computer Technology. Springer-Verlag Berlin. Alemania 438 pp.

IERS. (2016). International Earth Rotation Service. En línea. Disponible en: http://www.iers.org/

IAG-GGOS. (2016). International Association of Geodesy. On the Geodesy. En línea. Disponible en: http://www.iag-ggos.org

Jekeli, C. (2006). Geometric Reference System in Geodesy. Division of Geodesy and Geospatial Science. School of Earth Sciences. Ohio State University. 202 pp.

Leick, A. (2204). GPS Satellite Surveying. Editorial Wiley. Tercera Edición. Estados Unidos. 464 pp.

LGFS. (2016). Laboratorio de Geodesia Física y Satelital. Universidad del Zulia, Venezuela. En línea. Disponible en: http://www.lgfs.luz.edu.ve/

Lu, Z., Qu, Y. y Quiao, S. (2014). Geodesy Introduction to Geodetic Datum and Reference Systems. Springer Heidelberg New York Dordrecht London. DOI 10.1007/978-3-642-41245-5_5

Molodensky, M.S., Eremeev, V.F. y Yurkina, M. I. (1962). Methods for the Study of the External Gravitational Field and Figure of the Earth. Israeli Programme for the Translation of Scientific Publications, Jerusalem.

Moritz, H. (1979). Advanced Physical Geodesy. Wichmann. 500 pp.

NIMA. (2004). WGS84 definition/relationships with Geodetic Systems. Technical Report, No. 8350.2, National Imagery and Mapping Agency, Washington.

Rapp, R. (1991). Geometric Geodesy Part I. The Ohio State University. Department of Geodetic Science and Surveying. EE.UU. 189 pp.

Seeber, G. (2003). Satellite Geodesy. Walter de Gruyter-Berlin-New York. 589 pp.

SIRGAS. (2016). Sistema de Referencia Geocéntrico para las Américas (SIRGAS). En línea. Disponible en: http://www.sirgas.org

Torge, W. (1989). Gravimetry. Walter de Gruyter. Berlin, Alemania. 465 pp.

Torge, W. (2001). Geodesy. 3rd. Edition. Walter de Gruyter-Berlin-New York. 416 pp.

Wolf, H. (1963). Geometric connection and re-orientation of three-dimensional triangulation nets. Bulletin Geodesique, 68, 165-169.

---