Número 68(1) • Enero-junio 2022
ISSN: 1011-484X • e-ISSN 2215-2563
Doi: https://dx.doi.org/10.15359/rgac.68-1.13
Recibido: 13/03/2021 • Aceptado: 09/04/2021
URL: www.revistas.una.ac.cr/index.php/geografica/
Licencia (CC BY-NC-SA 4.0)
Consistencia, homogeneidad y distribución de la precipitación pluvial y temperatura, Región Sierra de Amula, Jalisco, México
Rainfall and temperature consistency, uniformity and distribution, Sierra de Amula region, Jalisco, Mexico
Jonatan Daniel Chávez De La Lima1
Universidad de Guadalajara, México
José Luis Olguín López2
Universidad de Guadalajara, México
Rubén Darío Guevara Gutiérrez3
Universidad de Guadalajara, México
Óscar Raúl Mancilla Villa4
Universidad de Guadalajara, México
Carlos Palomera García5
Universidad de Guadalajara, México
Gerardo Cruz Sandoval6
Universidad de Guadalajara, México
Resumen
De la base de datos de 34 años de las 92 estaciones distribuidas en la región Sierra de Amula en el estado de Jalisco–México se estimaron los datos mensuales faltantes de precipitación y temperatura a través de los métodos de media aritmética, regresión lineal simple y la técnica de la U.S. National Weather Service. La estimación de la consistencia y homogeneidad de esta base se realizó a través del análisis de doble masa, t de Student y Cramer, procesados mediante los Sistemas de Información Geográfica. Se rellenaron datos faltantes de hasta 36,036 para precipitación y 9,730 para temperatura, se presentaron errores de consistencia de los datos de precipitación en 10 meses, a excepción de julio y agosto, con una R2=0.99 (α=0.05); para la temperatura fue de R2=1 y una predicción y confianza al 100%. Se encontraron valores de t de Student y Cramer inferiores a 1.56, situación que determina homogeneidad y calidad (R2=0.99). El mejor método para interpolar la precipitación fue polynomial interpolation, para temperatura fue J-Bessel con una confiabilidad cercana a 100%.
Palabras clave: Sistemas de Información Geográfica; Cramer; t de Sstudent
Abstract
Missing monthly rainfall and temperature data were estimated to complete a 34-year meteorological record from 92 weather stations distributed in the Sierra de Amula region in the state of Jalisco, Mexico, by applying the methods of arithmetic mean, simple linear regression and the technique employed by the U.S. National Weather Service. Estimation of data consistency and homogeneity was achieved by means of double mass analysis, and Student’s t- and Cramér’s t-tests processed by Geographic Information Systems. Missing data was filled for up to 36,036 rainfall and 9,730 temperature data points. Data consistency errors were found for rainfall data of 10 months, with the exception of July and August, showing R2 = 0.99, (α = 0.05); for temperature, data exhibited R2 = 1 with a confidence and prediction of 100%. Student’s t- and Cramér’s t-test values below 1.56 were found and indicates a high degree of data homogeneity and quality (R2 = 0.99). The best method to interpolate rainfall data was polynomial interpolation, whereas for temperature, J-Bessel provides a reliability close to 100%.
Keywords: Geographic Information Systems; Cramér’s t-test; Student’s t-test.
La precipitación pluvial y temperatura ambiental son variables climáticas de gran importancia, registradas de forma regular en el territorio mexicano (Núñez-González & García-Suarez, 2018). Estos registros, con base en el Panel Intergubernamental sobre Cambio Climático (IPCC, 2007) han aumentado para el caso de las precipitaciones de 5 y 10% en latitudes medias y altas de los continentes del hemisferio norte, aunque también han disminuido en promedio de 3% sobre gran parte de las áreas subtropicales. Martínez-Austria y Aguilar-Chávez (2009) mencionan que el IPCC indica que, en México, por su ubicación geográfica, las precipitaciones disminuyen y las temperaturas aumentan lo que ocasiona elevada vulnerabilidad al clima. García (2003) y Campos (1992) mencionan que la precipitación varía en espacio y tiempo, geográficamente aumenta en dirección norte-sur debido a la influencia de la latitud y su proximidad al océano Pacifico y Golfo de México, así como por la orografía y rasgos de la circulación atmosférica. Mosiño y García (1974) manifiestan que estas condiciones influyen sobre 70% de la distribución de la precipitación pluvial entre los meses de mayo a octubre, condición que Greenpeace (2010) e INECC (2016) estiman que, para el caso del estado de Jalisco–México, se produzca una reducción de la precipitación total anual de 5 a 10% para el 2020 y de 5 a 15% para 2080.
El estudio de homogeneidad, tendencia, variabilidad de la precipitación pluvial y la temperatura a nivel regional es de vital importancia para planificar el manejo de los recursos naturales, además de apoyar la evaluación de la calidad climática (Méndez-González, Návar-Cháidez & González-Ontiveros, 2008). Ayllón (2003) plantea que la forma más fácil de analizar e interpretar el clima en términos de medias anuales o estacionales de temperatura y/o precipitación es a través de series de tiempo; no obstante, Alfaro y Soley (2008) y Núñez-González y García-Suarez (2018) reconocen que, para trabajar con series de tiempo meteorológicas, la falta de una base de datos completa complica el análisis, por lo tanto, es indispensable contar series de tiempo que reúnan las condiciones de calidad. El cálculo homogeneidad y tendencia de la precipitación pluvial y temperatura ambiental surge de la necesidad de conocer la variación de estos parámetros climáticos, para ello, se considera para el cálculo cuatro etapas fundamentales: 1) relleno de datos faltantes de precipitación y temperatura por un periodo de 34 años (1980 al 2013), 2) corrección de los mismo utilizando curvas de doble masa, y 3) análisis de homogeneidad o consistencia de la serie cronológica útil en la obtención de la tendencia y distribución espacial de las variables climáticas. Al respecto, Thom (1971) indica que una serie de datos es llamada homogénea si es una muestra de una única población; si la serie es inhomogénea, se le deben hacer ajustes y correcciones para volverla homogénea.
El estudio propuesto será de vital importancia en la elaboración de análisis de tendencia en las variables del clima como la precipitación y temperatura; además de la distribución espacial del clima en la región Sierra de Amula, considerando que en la actualidad no existe información alguna a esta escala geográfica. Por lo tanto, los resultados obtenidos en este trabajo se consideran la base principal para encontrar la relación del clima con las diferentes actividades humanas y ecosistemas naturales.
Descripción de la zona de estudio
La región Sierra de Amula (Figura 1) se encuentra entre los 19° 20' a 20° 40' norte y 103° 40' a 104° 50' oeste, al oeste del estado de Jalisco, conformada por 14 municipios.
Figura 1. Ubicación de la zona de estudio, INEGI 2018
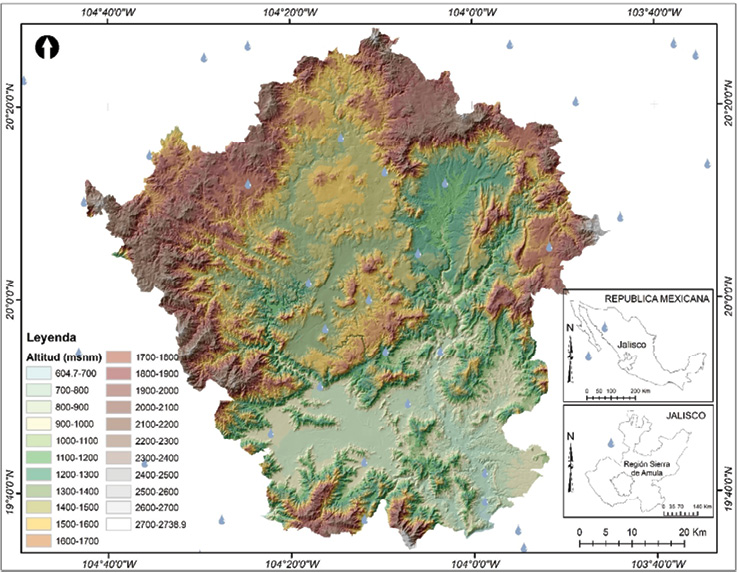
Fuente: Elaboración propia.
Distribuidos sobre una superficie de 5,788.3 km2 y rango de 604.7 a 2,738.9 msnm, precipitación pluvial anual promedio de 914 mm y temperatura extrema de 7 a 20.9°C. La geomorfología es muy diversa, caracterizada por zonas de montaña con presencia de sierras con vegetación de clima frío, mesetas con pequeños lomeríos hasta grandes valles formados por roca volcánica extrusiva ácida en su mayor parte (IIEG, 2018); los suelos presentes son Regosoles, Feozem y Litosoles, que constituyen más de 82.5% de la región (IIEG, 2018). Los tipos de cobertura vegetal dominantes de la región son bosque (17.6%), vegetación secundaria arbórea y arbustiva y selva baja caducifolia (37.9%), la selva baja caducifolia constituye 1.4%, y agricultura de temporal y riego (28.8%), actividad económica de gran importancia regional (INEGI, 2018).
Para la planeación de proyectos relacionados con el agua es necesaria la información climatológica proveniente de los elementos meteorológicos (precipitación y temperatura) (Mesa, Poveda & Carvajal, 1997); las predicciones realizadas en referencia a las condiciones meteorológicas propias de cada lugar dependen de la calidad y cantidad de la información, por lo que resulta necesario el análisis exploratorio de bases de datos con el fin de determinar cambios o tendencias, esencial de cualquier análisis estadístico y de evaluación previa de su estructura, consistencia y homogeneidad, que constituye un enfoque de caja negra que incrementa el grado de incertidumbre sobre la validez de los posibles resultados (Lobo, 2004).
Para describir la estadística de la base de datos es preciso recopilar información de orden cualitativa o cuantitativa perteneciente a grupos de individuos o fenómenos y deducir a partir del análisis de datos la respuesta a proyecciones futuras (Posada-Hernández, 2016). Los métodos empleados en la recolección, organización, resumen, análisis e interpretación de datos tienen el objetivo de validar las conclusiones y así poder tomar decisiones de manera razonable y efectiva (Spiegel, 2013). Por ello, es necesario que la base de datos de una muestra o población tienda a reunirse alrededor de un valor central o valor representativo (medida de tendencia central) como la media aritmética, la mediana y la moda (Walpole & Myers, 2012; Posada-Hernández, 2016). El seguimiento del análisis estadístico para el caso de los datos meteorológicos se considera la homogeneidad de la serie, y en análisis hidrológicos, la consistencia. Ambos términos son sinónimos que indican el cambio en la cantidad de lluvia medida por estación meteorológica. Sin embargo, su diferencia se establece en las técnicas empleadas: para la homogeneidad son utilizadas las pruebas estadísticas como la t de Student y Cramer, y para la consistencia, se detecta con la curva de doble masa, técnica que detecta y corrige las inconsistencias de un tiempo determinado (Campos, 1987).
La estimación de la homogeneidad, consistencia y distribución de la serie cronológica de los datos de precipitación pluvial y temperatura ambiental y su posterior manejo en los Sistemas de Información Geográfica (SIG) utilizando el software arcmap 10.5 se realizó a través del siguiente procedimiento.
Obtención de la información climática y de cartografía espacial
La información mensual y anual de los datos de precipitación pluvial y temperatura ambiente para 34 años (1980–2013) se obtuvo de 91 estaciones climatológicas de la base de datos climática de ERICIII V.3.2 del Instituto Mexicano de Tecnología del Agua (IMTA, 2016). La información cartográfica (curvas de nivel, uso de suelo y vegetación) necesaria para describir la zona de estudio se recabó del Instituto Nacional de Estadística y Geografía (INEGI, 2018).
Llenado de datos mensuales y anuales faltantes de precipitación y temperatura
La estimación de los datos faltantes se hizo en consideración a las estaciones climatológicas ubicadas dentro y en la periferia del área de estudio; para ello, se clasificaron las estaciones por rango de altitud de 0 a 450 msnm, 450 a 850 msnm, 850 a 1300 msnm, 1300 a 1850 msnm, 1850 a 2400 msnm, base a la que se aplicó la correlación entre estaciones y la media aritmética para cada estación que presente tres meses sin información y apoyadas de la base de datos de las estaciones más cercanas (Calvache & Duque, 2010). Cuando no fue posible aplicar este procedimiento, se utilizó la técnica de regresión lineal simple (Campos, 1987), tomando como referencia valores de correlación entre estaciones de 0.6 a 1. Al no lograr el llenado de la base de datos mensuales o anuales mediante los anteriores métodos, se aplicó la metodología de la U. S. National Weather Service (Campos, 1987):
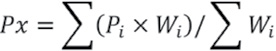
Donde: Pi corresponde a la precipitación observada para la fecha faltante en las estaciones auxiliantes circundantes (mm); Wi corresponde a 1/D2 siendo D igual a la distancia entre cada estación circundante y la estación incompleta (km).
Corrección y consistencia de datos pluviométricos y termométricos
La corrección de datos se efectuó mediante la técnica de doble masa (Calvache & Duque, 2010; Campos, 1987) que verifica la consistencia de la base de datos de las estaciones;además de generar métodos para corrección de datos del registro, en caso de presentar errores. Estos son: (a) la serie de puntos se ajustan a la línea recta (proporcionalidad y consistencia en la estación analizada), (b) ajuste de una serie de rectas paralelas en la que los puntos coinciden (proporcionalidad), aunque existan años que estén medios por exceso o por defecto, c () ajuste de dos rectas de diferente pendiente (caso típico de error sistemático), (d) cuando la estación presenta un tramo central de mayor o menor pendiente, se considera que 95% de los casos en tal periodo (años de registro) se midieron incorrectamente y habrá que corregir para homogeneizar la serie.
Homogeneidad de los datos climatológicos
Con base en la tendencia de los datos se aplicó la prueba estadística de homogeneidad, la que es aceptada o rechazada con base en su probabilidad de ocurrencia. Para el caso de probabilidad pequeña, se concluye que la serie cronológica fue inhomogénea, por el contrario, si la probabilidad es grande, la serie es homogénea (Thom, 1971). Campos (1987) indica que, cuando es posible especificar la distribución que sigue la hipótesis nula y alternativa, la aplicación de las pruebas paramétricas es lo más indicadas, por el contrario, se deben seleccionar las pruebas no paramétricas. Se consideró, por lo tanto, la aplicación de pruebas estadísticas que se aplican a los datos de la serie cuya homogeneidad se investiga.
a) Prueba estadística de t de Student: esta prueba es poderosa para detectar la inconsistencia en la media, además de ser un test robusto, excepto cuando la longitud de los dos periodos seleccionados para comparación de sus medias es desigual, pues entonces la distribución de los datos puede no ser sesgada. La prueba estadística está definida por la ecuación:
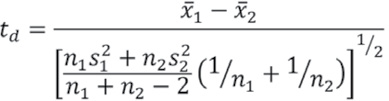
Donde: 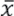 1 y
1 y 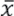 2 representan la media de los dos periodos para comparar, n1 y n2 corresponden al periodo de registro de los datos,
2 representan la media de los dos periodos para comparar, n1 y n2 corresponden al periodo de registro de los datos, 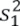 y
y 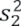 son las varianzas de xi en los dos periodos de registro respectivamente. Entonces,
son las varianzas de xi en los dos periodos de registro respectivamente. Entonces, 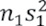 y
y 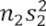 es calculada por la ecuación:
es calculada por la ecuación:
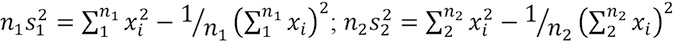
El valor absoluto de td se compara generalmente con el valor t de la distribución de Student de dos colas y con v = n1 + n2 – 2 grados de libertad y con 5% significancia. Si y solo si el valor absoluto de td es mayor que t, se concluye que la diferencia entre las medias es evidencia de inconsistencia o falta de homogeneidad. Los valores de t se encuentran en Campos 1987 capítulo 4.
b) Prueba estadística de Cramer: complementaria a la prueba de t de Student, investiga la homogeneidad, si conviene comparar la media de toda la serie y la media de una cierta parte del registro de datos. Esta prueba estadística es recomendable cuando n1 y n2 no son parecidos. En la prueba estadística utilizada son la media (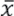 ) y la desviación típica (s) del registro total de n valores, y
) y la desviación típica (s) del registro total de n valores, y 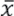 k es la media del subperiodo de n' valores.
k es la media del subperiodo de n' valores.
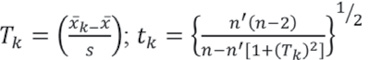
La estadística tk tiene distribución t de Student de dos colas con v = n – 2 grados de libertad y es utilizada en la misma forma que la estadística td.
Modelación espacial de la precipitación y temperatura
Realizada una vez estimados los datos faltantes de la base de datos mensuales y anuales de precipitación y temperatura, corrección, consistencia y homogeneidad de los datos para posteriormente utilizar el análisis estadístico descriptivo a través de las medidas de tendencia central (media, mediana) y las medidas de dispersión (varianza, desviación estándar y coeficiente de variación) para obtener información cualitativa y cuantitativa con la finalidad de obtener respuestas para el uso de los datos en la geoestadística aplicada a los Sistemas de Información Geográfica de las series de precipitación y temperatura.
La serie cronológica de precipitación y temperatura corresponde a 91 estaciones, 19 ubicadas dentro de la región en estudio (Tabla 1). La cobertura superficial por estación es de 321.6 km2. La Organización Meteorológica Mundial (OMM, 1970) para regiones montañosas de zonas templadas y tropicales en circunstancias excepcionalmente difíciles recomienda una densidad de cobertura de 250 a 900 km2 por estación.
Tabla 1. Estaciones climatológicas ubicadas en la región Sierra de Amula
|
Estación |
Periodo |
Coord. en X |
Coord. en Y |
Altitud (msnm) |
|
Atengo |
1979-2011 |
579,360.2 |
224,2649.0 |
1,400 |
|
Autlán |
1945-2013 |
565,997.5 |
218,6152.6 |
900 |
|
Chiquilistlán |
1964-1996 |
619,188.1 |
222,1848.1 |
1,700 |
|
Tacotán |
1947-2013 |
573,211.2 |
221,4954.3 |
1,330 |
|
Tecolotlán |
1942-2013 |
599,252.3 |
223,3897.7 |
1,200 |
|
Tenamaxtlán |
1970-2003 |
587,748.1 |
223,6049.1 |
1,470 |
|
Tuxcacuesco |
1961-2013 |
606,902.4 |
217,8604.7 |
720 |
|
Unión de Tula |
1926-2006 |
576,387.5 |
220,6114.4 |
1,340 |
|
Cuautla |
1979-2010 |
561,639.6 |
223,3723.1 |
1,720 |
|
Ejutla |
1940-2008 |
587,920.7 |
220,1741.4 |
1,140 |
|
El Chante |
1969-2013 |
583,833.3 |
218,0694.5 |
900 |
|
El Corcovado |
1974-2013 |
575,388.4 |
219,5043.3 |
900 |
|
El Grullo |
1939-1991 |
575,388.4 |
219,5043.3 |
905 |
|
El Limón |
1984-1944 |
592,159.6 |
219,1802.7 |
822 |
|
El Rosario |
1980-2013 |
606,935.6 |
217,3071.2 |
700 |
|
Ixtlahucan de S. |
1980-2012 |
584,732.4 |
221,1686.2 |
1,460 |
|
Juchitlán |
1948-2013 |
594,100.0 |
222,0587.9 |
1,230 |
|
Manantlán |
1965-1995 |
583,885.3 |
216,9628.1 |
1,450 |
|
Presa Basilio Badillo |
1978-2013 |
598,388.1 |
220,1796.8 |
824 |
Fuente: Elaboración propia.
Llenado de datos faltantes
El porcentaje inicial de los datos mensuales de precipitación pluvial fue de 70%, el 30% del vacío de datos se estimó por estación climatológica, equivalente a 36,036 datos. Para registros mensuales de temperatura se recopiló 73%, para completar la serie al 100%, se estimaron 9,730 datos. Este llenado del registro para los 30 años (1980-2013) favorece y justifica su manejo para realizar estudios climáticos que apoyen: proyectos productivos, optimización de recursos, reducción del riesgo de pérdida en cosechas, planificación integral de la infraestructura de riego y drenaje, y la posible predicción climática (Toro-Trujillo, Arteaga-Ramírez, Vázquez-Peña & Ibáñez-Castillo, 2015). Algunos estudios pueden adecuarse a registros incompletos, pero no así estudios de homogeneidad y consistencia cronológica de serie de tiempo, los cuales requieren una serie completa (Alfaro & Soley, 2008). Las estaciones que presentaron las series completas (Tabla 2), fueron utilizadas en estudios de consistencia y homogeneidad o para estimar datos de precipitación pluvial o temperatura a través del uso de la regresión lineal simple (Calvache & Duque, 2010).
Tabla 2. Correlación de Pearson para los datos anuales a rellenar.
|
Xi |
Yi |
Precipitación |
Xi |
Temperatura |
|
Tenamaxtlán |
Atengo |
0.75 |
Zacoalco de torres |
0.98 |
|
Acatlán de Juárez |
Autlán |
0.69 |
El Grullo |
0.60 |
|
El algodonal |
Chiquilistlán |
0.62 |
El Grullo |
0.80 |
|
I. de Santiago |
Tacotán |
0.78 |
M.M. Meduiguez |
0.98 |
|
Juchitlán |
Tecolotlán |
0.68 |
Cumbre de Gpe. |
0.85 |
|
Mixtlán |
Tenamaxtlán |
0.60 |
Atengo |
0.86 |
|
C. V. Carranza |
Tuxcacuesco |
0.67 |
El Rosario |
0.61 |
|
Av. Camacho |
Unión de Tula |
0.72 |
Acatlán |
0.60 |
|
Concepción de Bnos. Aires. |
Cuautla |
0.54 |
Cajón de Peña |
0.70 |
|
I. de Santiago |
Ejutla |
0.78 |
La vega |
0.66 |
|
Manantlán |
El Chante |
0.80 |
C. V. Carranza |
0.65 |
|
Autlán |
El Corcovado |
0.71 |
Ahualulco de Mercado |
0.73 |
|
Unión de Tula |
El Grullo |
0.73 |
Chiquilistlán |
0.80 |
|
Concepción de Bnos. Aires. |
El Limón |
0.64 |
El Corcovado |
0.77 |
|
El Rodeo |
El Rosario |
0.60 |
Tuxcacuesca |
0.63 |
|
Av. Camacho |
I. de Santiago |
0.60 |
El Nogal |
0.67 |
|
I. de Santiago |
Juchitlán |
0.60 |
Cumbre de Gpe. |
0.60 |
|
Gargatillo |
Manantlán |
0.61 |
Atengo |
0.71 |
|
Cuautla |
Pres Basilio Badillo |
0.62 |
Canoas |
0.89 |
Las estaciones con variable independiente se utilizaron para obtener datos faltantes de las estaciones dependientes. Fuente: Elaboración propia.
Análisis y corrección mediante la técnica doble masa
Los gráficos de doble masa para los datos promedio mensuales de precipitación en 34 años del periodo de registro (ajuste de series) únicamente en los meses de julio y agosto no registraron algún tipo de error (Figura 2). La distribución de los puntos sobre la línea de tendencia sugiere proporcionalidad y consistencia de los meses analizados; comportamiento debido al mayor número de eventos y cantidad de precipitación registrada.
Figura 2. Análisis de doble masa para los meses de julio y agosto.
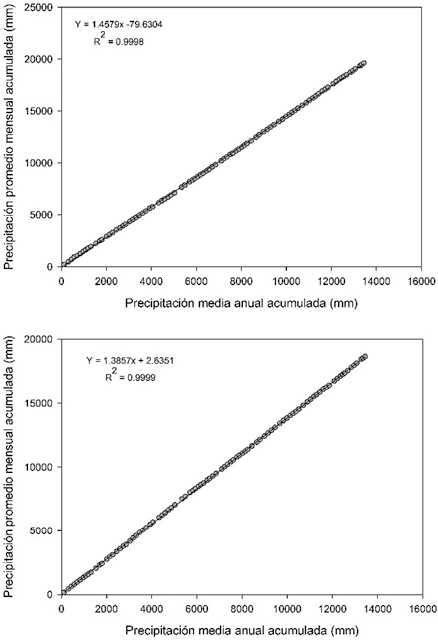
Fuente: Elaboración propia.
Los datos de los meses restantes (en orden cronológico) presentan errores de calidad de los datos (Figura 3) donde la distribución de los puntos (mayor de 5) no se ajusta sobre la línea de tendencia, con datos medidos por exceso o defecto (Campos, 1987); a pesar de encontrar correlaciones (R2) cercanas a la unidad.
Figura 3. Análisis (izquierda) y corrección (derecha) de los datos de precipitación para los meses representativos de enero y abril
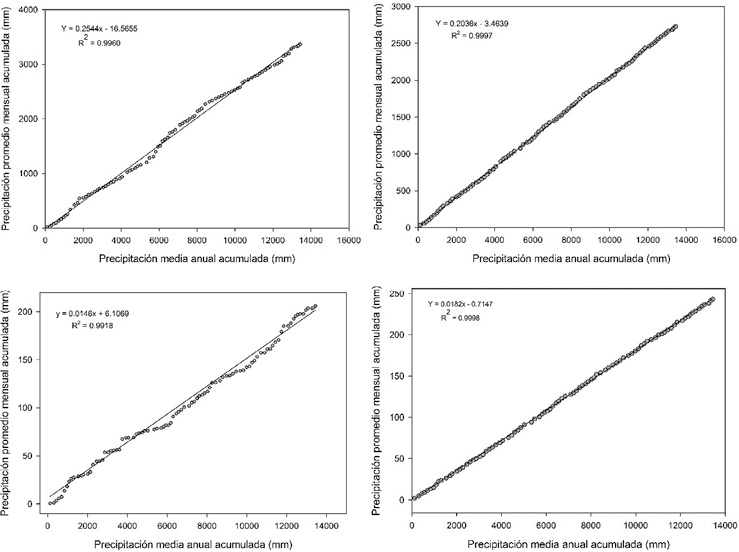
Fuente: Elaboración propia.
El registro de menor calidad fue para el mes de abril (R2=0.9918), posterior al ajuste se obtiene una distribución casi perfecta (Figura 3) donde los puntos se distribuyen sobre la pendiente de la línea de tendencia con algunos datos (menos de 5 puntos) medidos por exceso o por defecto, lo que indica el aumento en la correlación (R2) con α = 0.5. Los datos corregidos de precipitación mensual de 10 meses (sin considerar julio y agosto) reflejan proporcionalidad y consistencia en el registro de datos.
Para los datos mensuales de temperatura (Figura 4) se registraron errores leves (caso B, inciso 3 del marco metodológico) en los 12 meses del año. Para enero y diciembre (en orden cronológico) se presentan datos medidos por exceso o defecto, principalmente en la parte media de la línea de tendencia (>5 puntos), esta situación requirió la corrección de los datos a través de la obtención de correlaciones elevadas cercanas a la unidad.
Figura 4. Análisis (izquierda) y corrección (derecha) de enero y diciembre
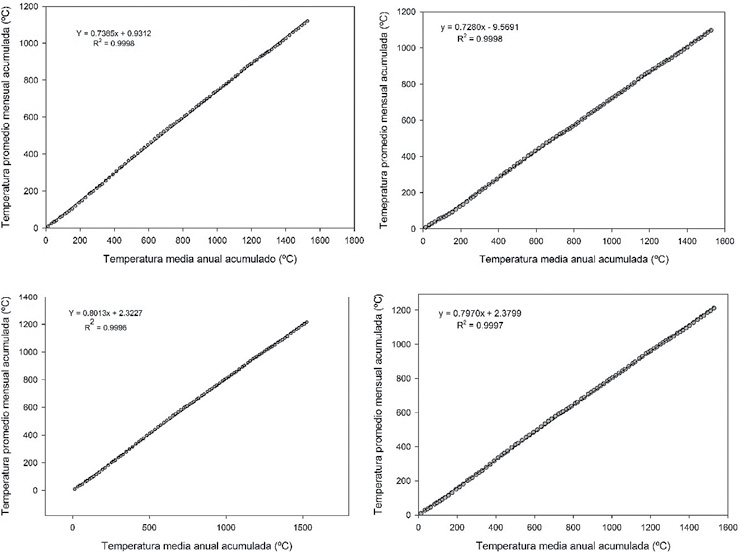
Fuente: Elaboración propia
Con respecto a los resultados de temperatura de los meses febrero a noviembre (en orden cronológico) (Figura 5), no fue necesaria su corrección debido a que los puntos se distribuyen sobre la línea de tendencia, que reflejan una predicción y confianza de 95% de probabilidad (α = 0.05); cada estación correspondiente refleja proporcionalidad y consistencia.
Figura 5. Análisis de doble masa para los meses representativos de abril y julio
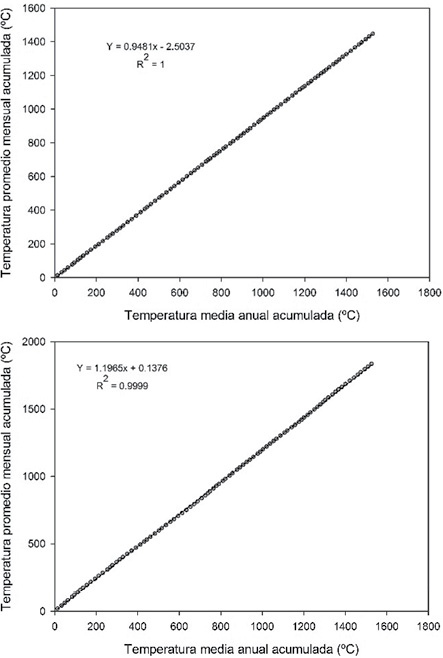
Fuente: Elaboración propia.
Castro-Lina y Carbajal-Escobar (2010) y Mesa et al. (1997) establecen que las predicciones, planeación y diseño de proyectos relacionados con el agua dependen de la cantidad y calidad de la información. Se determina que la información aquí expuesta cumple con las expectativas en cuanto a la proporcionalidad de la serie de precipitación y temperatura.
Análisis de homogeneidad
Para el análisis climatológico, la información corregida fue explorada usando métodos gráficos y estadísticos cuantitativos; al no realizar el procedimiento mencionado, se indica que los resultados obtenidos no cumplen con los criterios de independencia, normalidad, homogeneidad; modelando la serie cronológica de forma incorrecta (Maidment, 1993). Este mismo autor indica que los métodos gráficos, como herramienta exploratoria de los datos, se usan con dos propósitos: revelar las características de una posible distribución o las relaciones que existen entre las variables, que de otra manera no podrían ser descubiertas.
Los valores de t de Student y Cramer para los doce meses se presentan en la siguiente figura (izquierda) encontrando las cifras máximas para t de Student en los meses de mayo y septiembre para el registro de precipitación; para la temperatura fue en los meses de enero y diciembre. Esta situación puede sugerir que existe un cambio abrupto en las medias, pero sin considerarse como registros inhomogéneos. En este sentido, se concluye que los valores absolutos de t-Student y Cramer no rebasan el valor límite encontrado en la distribución de t de Student de dos colas, con 98 grados de libertad y un nivel de significancia (α = 0.05); se considera que el registro de precipitación y temperatura son homogéneos.
Figura 6. Resultados de t de Student y Cramer para los datos mensuales
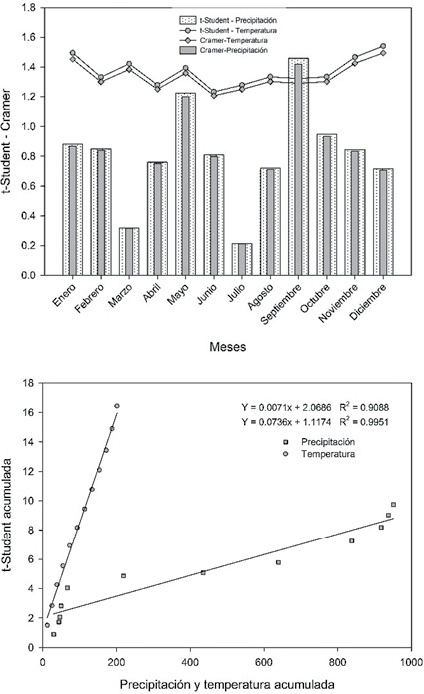
Fuente: Elaboración propia.
De forma similar se observa que los resultados obtenidos de los registros mensuales de temperatura y precipitación tienen el mismo comportamiento para t de Studen y Cramer, aunque en esta última se considera complementaria a la t de Student (Campos, 1987), para ello se requiere comparar la media de la serie y la media de una parte del registro para determinar homogeneidad. En la figura anterior (derecha), en la correlación de las medias mensuales de las variables climáticas del periodo de registro se obtiene un mejor ajuste de los datos de temperatura sobre la información encontrada de t de Student, la distribución de los puntos sobre la línea de tendencia es más aceptable en comparación con la distribución de la precipitación.
Modelo espacial de precipitación y temperatura
Para la distribución espacial de las variables climáticas, la estadística y geoestadística fue importante en el sentido de la toma de decisiones efectivas y pertinentes para la selección del método de interpolación a utilizar (Barreto-Villanueva, 2012). La modelación espacial de la información sin previa evaluación de su estructura, consistencia y homogeneidad; constituye un enfoque de caja negra que incrementa el grado de incertidumbre sobre la validez de los resultados (Lobo, 2004). Los datos mensuales de precipitación presentan distribución normal, con diferencias entre la media y mediana menor a la unidad para los primeros cinco y últimos dos meses del año (Tabla 3). Ello significa que 50% de los datos se distribuyen a los costados del punto medio, condición que permite no realizar cambios en los SIG (transformación logarítmica, semivariograma, anisotropía) para ser interpolados.
Tabla 3. Análisis estadístico en los datos mensuales de precipitación
|
Mes |
Media |
Mediana |
Error Estándar |
Curtosis |
Asimetría |
|
Enero |
30.0 |
30.0 |
0.9 |
7.1 |
2.1 |
|
Febrero |
14.0 |
13.3 |
0.3 |
2.0 |
0.8 |
|
Marzo |
3.2 |
3.2 |
0.1 |
-0.6 |
0.1 |
|
Abril |
3.0 |
2.6 |
0.1 |
-0.5 |
0.3 |
|
Mayo |
17.1 |
17.0 |
0.3 |
0.9 |
0.4 |
|
Junio |
152.6 |
149.2 |
0.3 |
0.6 |
0.5 |
|
Julio |
215.5 |
208.4 |
3.3 |
6.2 |
1.7 |
|
Agosto |
205.0 |
192.0 |
6.8 |
1.9 |
1.1 |
|
Septiembre |
198.7 |
182.0 |
7.0 |
0.6 |
0.9 |
|
Octubre |
79.4 |
74.9 |
3.0 |
1.7 |
0.9 |
|
Noviembre |
20.0 |
20.0 |
0.7 |
0.8 |
0.6 |
|
Diciembre |
13.4 |
12.9 |
0.3 |
0.4 |
0.6 |
Fuente: Elaboración propia.
Los datos de junio a octubre requirieron ser ajustados en los SIG (análisis geoestadístico) por no presentar similitud en la media y mediana, además presentan valores alejados a cero para curtosis y asimetría; situación que permitió la correcta interpolación espacial creando una superficie continua de la precipitación utilizando el modelo y confiabilidad que mejor se ajustó (Dressler et al., 2000) a la región Sierra de Amula (Figura 7).
Se observan valores altos en las zonas altas ocupadas por relieve de montaña principalmente incrementándose sobre todo en los meses de junio a octubre distribuidos principalmente en superficies ubicadas en la parte suroeste de la región; este periodo de 5 meses se considera como la temporada lluviosa del año. De los doce meses del año, enero registra una distribución de la precipitación muy marcada sobre altitudes bajas debido posiblemente a la influencia de vientos húmedos ingresando a la región por la parte sureste, este comportamiento de la precipitación también se observa sobre los meses de febrero a mayo. El método geoestadístico que mejor se ajustó fue el kriging tipo simple solamente en los meses lluviosos de junio a octubre, para mejorar el porcentaje de confiabilidad se relacionó juntamente con la altitud en msnm.
Figura 7. Distribución espacial de la precipitación sobre los meses representativos
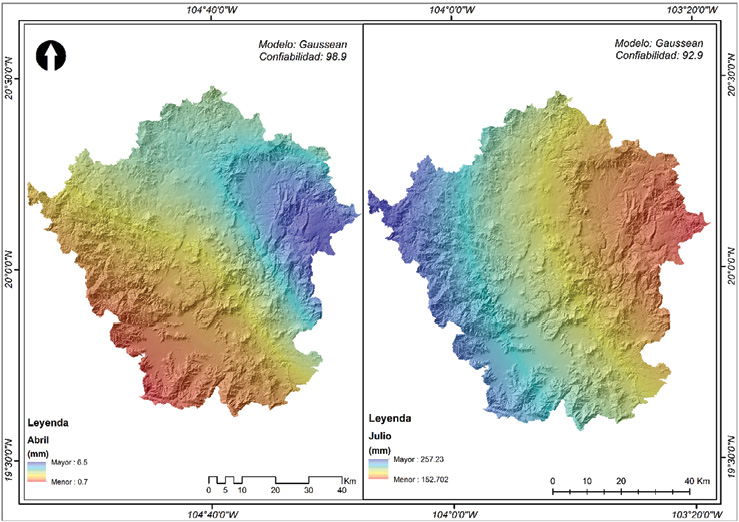
Fuente: Elaboración propia
Para el caso de los registros mensuales de temperatura, estos presentan una distribución normal (Tabla 4), respuesta reflejada a través de la aplicación de las medidas de tendencia central (media y mediana) que presentan una diferencia menor a la unidad; además su distribución simétrica es cercana a cero con tendencia negativa. Por lo que se considera no realizar la transformación logarítmica de datos para integrar los modelos de interpolación.
Tabla 4. Análisis estadístico en los datos mensuales de temperatura
|
Mes |
Media |
Mediana |
Error Estándar |
Curtosis |
Asimetría |
|
Enero |
12.3 |
12.6 |
0.4 |
-1.1 |
-0.04 |
|
Febrero |
12.7 |
13.0 |
0.4 |
-1.0 |
-0.2 |
|
Marzo |
13.8 |
14.1 |
0.4 |
-1.0 |
-0.3 |
|
Abril |
15.9 |
16.8 |
0.3 |
-1.0 |
-0.4 |
|
Mayo |
18.4 |
19.0 |
0.3 |
-1.0 |
-0.5 |
|
Junio |
20.5 |
21.2 |
0.3 |
-0.4 |
-0.6 |
|
Julio |
20.5 |
20.6 |
0.3 |
-1.0 |
-0.5 |
|
Agosto |
20.0 |
20.4 |
0.3 |
-1.0 |
-0.5 |
|
Septiembre |
19.8 |
20.1 |
0.3 |
-1.0 |
-0.5 |
|
Octubre |
18.6 |
18.9 |
0.4 |
-1.0 |
-0.3 |
|
Noviembre |
15.8 |
15.9 |
0.4 |
-1.2 |
-0.2 |
|
Diciembre |
13.4 |
13.6 |
0.4 |
-1.2 |
-0.03 |
Fuente: Elaboración propia.
La distribución espacial de la temperatura registra valores altos en zonas con relieve bajo (Figura 8), y valores bajos en zonas altas sugiriendo que la interpolación se ajusta al patrón del relieve existente en la región.
Figura 8. Distribución espacial de la temperatura en los meses representativos
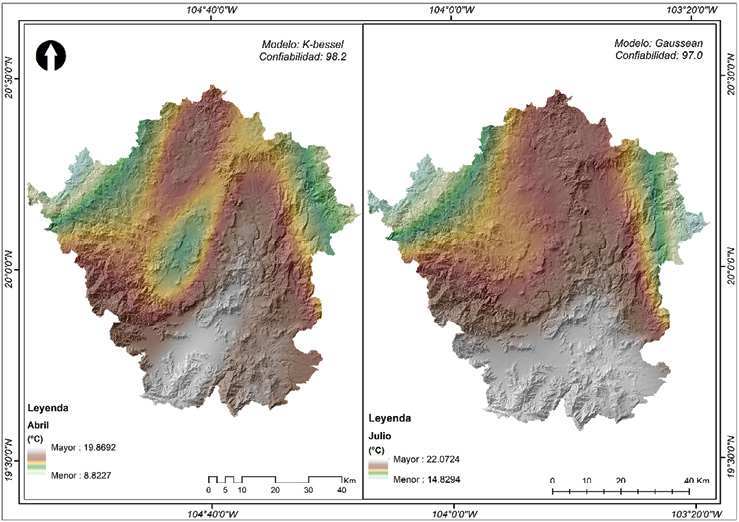
Fuente: Elaboración propia.
Su distribución presenta un comportamiento semejante para los meses de noviembre a abril con temperaturas máximas al sur y para los meses restantes se observa un aumento de la temperatura en la parte norte, bajo este contexto se considera que existe influencia de la zona costera sobre su distribución. En cuanto a los métodos utilizados para su interpolación, el método geoestadístico mejor evaluado fue kriging tipo simple con una confiabilidad arriba del 97% presentando errores en los modelos por abajo del 3%. En el caso de la precipitación y temperatura anual en la región, el mejor ajuste para la primera variable en su distribución espacial fue para el método determinístico utilizando la herramienta (local polynomial interpolation) presentando un error cuadrático medio de 177.4 con una confiabilidad cercana al 100% (Figura 9). La precipitación presenta valores máximos en la parte sur y oeste (municipio de Autlán de Navarro, Ayutla y Cuautla); este comportamiento puede deberse a la cercanía de la zona costera debido al porcentaje alto de humedad relativa que es transportada por el viento.
Figura 9. Distribución espacial de la precipitación y temperatura
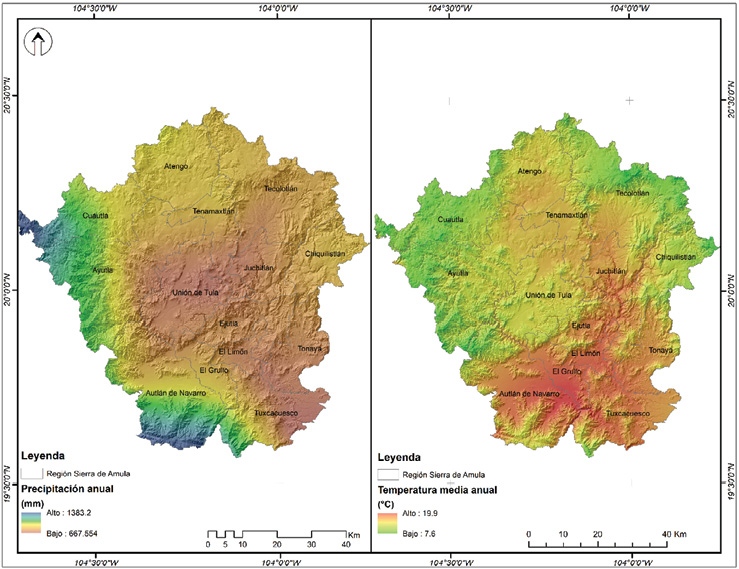
Fuente: Elaboración propia.
Las mínimas precipitaciones se presentan al centro y este de la región, debido a los vientos secos provenientes del norte y centro de la República Mexicana, así como a la franja montañosa, que intersecta las Sierra Madre Occidental, Sierra Madre del Sur y el Eje Neovolcánico, barreras naturales que impiden el libre ingreso de vientos cálidos provenientes de la costa. Rodríguez-Jiménez, Benito-Capa y Portela-Lozano (2004) mencionan que las montañas obligan al aire húmedo a subir de altitud provocando precipitaciones en barlovento y tiempo fresco y seco en sotavento. La distribución espacial de la temperatura fue interpolada utilizando el método geoestadístico kriging tipo ordinario bajo el modelo J-Bessel con una confiabilidad del 98.4% y un error cuadrático medio de 1.5. Para obtener los resultados anteriores se utilizó la variable altitud en msnm, donde los valores altos se distribuyen en relieves y cañadas con altitud baja principalmente en la parte sur de la región. Valores bajos se distribuyen sobre relieves altos (Figura 9) en la zona norte, noroeste y noreste de la región. La variación entre valores máximos y mínimos es aproximada a 12 °C influenciada por las zonas montañosas. IPCC (2007) indica que la variabilidad es mayor a escala regional que a escala mundial, debido a que influyen factores no climáticos como lo son los cambios de uso de la tierra (deforestación, la agricultura extensiva de temporal) que pueden inferir sobre el clima de una región en particular. En este sentido, Andrade-Martínez et al., (2019) expresan que existe una relación positiva entre el incremento de la temperatura y la producción de granos básicos (maíz y frijol), por lo tanto, zonas con valores arriba de los 20 °C a 21.6 °C la producción aumenta significativamente. Sin embargo, Stöckle et al., (2010) mencionan que en una superficie con presencia de temperaturas bajas la germinación, desarrollo y crecimiento de los cultivos son reducidos; situación que se presenta sobre superficies de montaña principalmente al norte dentro de la región Sierra de Amula (Figura 9). Para INIFAP (2013) la germinación, desarrollo y producción optima se reflejan en temperaturas de 13 a 30 °C, por el contrario, cuando hay valores inferiores a 12 la actividad fisiológica del cultivo se reduce o posiblemente es nula.
Al clasificar las estaciones mediante rangos de altitud para rellenar datos faltantes de precipitación y temperatura, las técnicas empíricas son más eficaces en su estimación. Así como en la eficiencia de los resultados al utilizar el análisis de doble masa para la corrección del registro; éstos se presentaron principalmente en los registros mensuales de precipitación a diferencia de los registros de temperatura, respuesta debida posiblemente a la dependencia de la precipitación a factores climáticos como el viento, relieve, temperatura y humedad relativa, entre otros. Se considera que la metodología establecida para encontrar la consistencia y homogeneidad de los datos fue acertada obteniendo valores por debajo de 1.56 para t de Student y Cramer con 98 grados de libertad y un α = 0.05 lo cual significa homogeneidad y calidad de los datos. Finalmente, el método kriging tipo simple cumple con los términos de calidad y confiabilidad en la distribución espacial de las variables climáticas; aunado a que la base de datos obtenida y analizada cumple con los requerimientos de calidad en estudios de tendencia de la precipitación y temperatura.
La distribución espacial de la precipitación y temperatura en la región de estudio es de gran utilidad en la planeación de los recursos naturales agua, suelo y planta; tal como lo mencionan Maas y García-Oliva (1990), Pagiola (1999) y De Graaf (2001) indicando la importancia de obtener diagnósticos de la variación de las variables climáticas y su influencia sobre los cambios de uso de suelo como la erosión, sedimentación, azolves e inundaciones, entre otros. Suárez-Venero (2014) utiliza las distribuciones de las variables climáticas a nivel región para los estudios de zonificación agroecológica porque constituyen herramientas para darle respuesta al problema de realizar cambios en el uso de suelo y así evitar problemas generalizados de sub-uso y sobreuso del suelo, además de influenciar la planeación del uso de la tierra como instrumento para lograr un mejor aprovechamiento del suelo en función de la sostenibilidad económica, ecológica y social. Velázquez-Ruíz, Martínez-Rivera y Carrillo-González, (2012) elaboran una distribución espacial del clima de Koppen modificado por García en Bahía de Banderas donde se incluye la precipitación y temperatura con la finalidad de establecer una planeación del uso del suelo en regiones con problemas de erosión y como investigación de alternativas de uso del territorio en zonas agrícolas. Finalmente, García-Hernández, Perez-Magaña, Martínez-Corona y Gutiérrez-Villalpando (2020) obtienen la distribución espacial de la precipitación y temperatura y su impacto sobre el cambio de uso de suelo para determinar los procesos relacionados con la degradación de suelo y pérdida de biodiversidad y variabilidad climática; a su vez, Andrade-Martínez et al. (2019) realizan una aptitud de la superficie del suelo en la cuenca de Autlán, Jalisco, considerando las variables climáticas antes mencionadas y logra realizar una planificación del territorio para establecer cultivos básicos.
Alfaro, E. J. & Soley F. G. (2008). Descripción de dos métodos de rellenado de datos ausentes en series de tiempo meteorológicas. Revista de matemática, 16 (1), 60-75.
Andrade-Martínez E., De Niz-Lara, E. M., Benítez-Muñoz, M. A., Olguín-López, J. L., Guevara-Gutiérrez, R. D., Meza-Rodríguez, D., & Villalvazo-López, V. M. (2019). Identificación de zonas aptas para la agricultura de temporal con maíz y frijol en la cuenca de Autlán, Jalisco, México. Revista Geográfica de América Central, 1 (62), 17-48.
Ayllón, T. (2003). Elementos de Meteorología y Climatología. México: Trillas.
Barreto-Villanueva, A. (2012). El progreso de la estadística y su utilidad en la evaluación del desarrollo. Papeles de población, 18 (73), 241-271.
Calvache, M.L. & Duque, C. (2010). Prácticas de Hidrogeología. Granada, España: Editorial Universidad de Granada.
Campos, A. D. F. (1987). Procesos del ciclo hidrológico. San Luis Potosí, México: Editorial Universitaria Potosina.
Campos, A. D. F. (1992). Procesos del ciclo hidrológico. San Luis Potosí, México: Editorial Universitaria Potosina.
Castro-Lina, M. & Carbajal-Escobar, Y. (2010). Análisis de tendencia y homogeneidad de las series climáticas. Ingeniería de Recursos Naturales y del Ambiente, (9),15-25.
De Graaf, J. (2001) Downstream effects of land degradation and soil and water conservation. Background paper 5. Roma: FAO
Dressler, K. A., S. R. Fassnacht, R. C. Bales, R. E. David, D. Lampkin, & D. E. Myers. (2000). Geostatistical interpolation of point-measured SWE in the Colorado River Basin. EOS Transactions. AmericanGeophysical Union, 81 (48), 397.
García, E. (2003). Distribución de la precipitación en la República Mexicana. Investigaciones geográficas, (50), 67-76.
García-Hernández, M., Perez-Magaña, A., Martínez-Corona, B., & Gutiérrez-Villalpando, V. (2020). Cambio de uso de suelo y variabilidad en Chiautzingo, Puebla, México. Revista Iberoamericana de Bioeconomía y Cambio Climático, 6 (11), 1-11. doi: http://doi.org/10.5377/ribcc.v6i11.9421
Greenpeace. (2010). Jalisco y el cambio climático. Autor Recuperado de: https://nanopdf.com/download/jalisco-y-el-cambio-climatico_pdf
Instituto de Información Estadística y Geográfica del Estado de Jalisco (IIEG, 2018). Autlán de Navarro; Diagnostico del municipio. Autlán, Jalisco. Instituto de Información Estadística y Geografía. Recuperado de: http://iieg.gob.mx/contenido/Municipios/AutlandeNavarro.pdf
Instituto Nacional de Estadística, Geografía e Informática (INEGI, 2018). Conjunto de datos vectoriales escala 1:50000. Instituto Nacional de Estadística y Geografía Recuperado de: https://www.inegi.org.mx/app/mapas/
Instituto Nacional de Ecología y Cambio Climático. (INECC, 2016). El cambio climático en México: información por estado y por sector. Instituto Nacional de Ecología y Cambio Climático. Recuperado de: https://www.gob.mx/inecc
Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP, 2013). Requerimientos agroecológicos de los cultivos. Jalisco, México: Instituto Nacional de Investigaciones Forestales Agrícolas y Pecuarias-CIRPAC-Campo Experimental Centro Altos de Jalisco.
Instituto Mexicano de Tecnología del Agua (IMTA, 2016). Base de datos climatológica ERICIII, versión 3.2.
Gitay, H.; Suárez, A.; Dokken, D. J. & Watson R. T. (2002). Cambio climático y biodiversidad. Documento técnico V del IPCC. Grupo Intergubernamental de Expertos sobre el Cambio Climático OMM, WMO, PNUMA, UNEP. Recuperado de: https://archive.ipcc.ch/pdf/technical-papers/climate-changes-biodiversity-sp.pdf
Grupo intergubernamental de expertos sobre el cambio climático. (2007). Cambio climático: Informe de síntesis. Contribución de los Grupos de trabajo I, II y III al Cuarto Informe de Ginebra, Suiza.
Lobo, L. (2004). Guía metodológica para la delimitación del mapa de zonas áridas, semiáridas y subhúmedas secas de América Latina y el Caribe. Recuperado de: https://www.cazalac.org/publico/fileadmin/templates/documentos/Guia_metodologica_Mapa_ZA_ALC.pdf
Maass, J. M. & García-Oliva, F. (1990) La conservación de suelos en zonas tropicales: el caso de México. Ciencia y Desarrollo, XV (90), 21-36.
Maidment, D.R. (1993). Handbook of Hydrology. New York, US, McGraw Hill.
Martínez-Austria, P. F. & Aguilar-Chávez, A. (2009). Efectos del cambio climático en los recursos hídricos de México. Volumen II, México, SEMARNAT-IMTA. Recuperado de: https://www.imta.gob.mx/potamologia/images/docs/evento/PolioptroMartinez_CarlosPatino.pdf
Mosiño, P. A. & García, E. (1974). The climate of Mexico. World survey of climatology. In R. A. Bryson y F. K. Hare (eds.), vol. II, Climates of North America. London: Elsevier, 345-404.
Méndez-González, J., Návar-Cháidez, J. J., & González-Ontiveros, V. (2008). Análisis de tendencias de precipitación (1920-2004) en México. Investigaciones Geográficas (mx), (65), 38-55.
Mesa, O., Poveda, G. & Carvajal, L. (1997). Introducción al clima de Colombia. Bogotá, Colombia: Imprenta Universidad Nacional de Colombia.
Núñez-González, G. & García-Suárez, J. (2018). Análisis de la calidad de los datos y la tendencia de algunos índices de precipitación en el estado de Jalisco. Revista internacional de estadística y geografía, 9 (2), 14–27.
Organización Meteorológica Mundial (OMM). (1970). Guía de prácticas hidrometeorológicos. Ginebra, Suiza: Secretaría de la OMM.
Pagiola, S. (1999). The global environmental benefits of land degradation control on agricultural land. Washington D.C., US: World Bank Environment Paper nº 16.
Posada-Hernández, J. G. (2016). Elementos básicos de estadística descriptiva para el análisis de datos. Medellín, Colombia: Editorial Luis Amigo.
Rodríguez-Jiménez, R. M., Benito-Capa, A. & Portela-Lozano, A. (2004). Meteorología y Climatología. Madrid, España: Fundación Española para la Ciencia y la Tecnología.
Spiegel, M. R. (2013). Probabilidad y estadística. (4a ed.). New York, US: McGraw-Hill.
Stöckle, C., Nelson, R., Higgins, S., Brunner, J., Grove, G., & Boydston, R. (2010). Assessment of Climate Change Impact on Eastern Washington Agriculture. Climatic Change, 102 (1-2), 77-102.
Suárez-Venero, G. M. (2014). Apuntes sobre la zonificación agroecológica de los cultivos. Particularidades en Cuba. Cultivos tropicales, 35 (4), 36-44.
Thom, H. C. S. (1971). Some methods of climatological analysis. Technical Note No. 81, WMO-No. 199. TP. 103. Secretariat of the world meteorological organization. Geneva, Switzerland.
Toro-Trujillo, A. M., Arteaga-Ramírez, R., Vázquez-Peña, M.A. Ibáñez-&Castillo, & L.A. (2015). Relleno de series diarias de precipitación, temperatura mínima, máxima de la región norte de Urabá Antioqueño. Revista Mexicana de Ciencias Agrícolas, 6 (2), 577-588.
Velázquez-Ruíz, A., Martínez-Rivera, L. M., & Carrillo-González, F. M. (2012). Caracterización climática para la región de Bahía de Banderas mediante el sistema de Koppen, modificado por García y técnicas de sistema de información geográfica. Investigaciones Geográficas, (79), pp. 7-19.
Walpole, R. E., & Myers, R. H. (2012). Probabilidad y estadística. México: McGraw-Hill.
1 Ingeniero en Recursos Naturales y Agropecuarios. Departamento de Ecología y Conservación de la Biodiversidad. Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: Daniel.chavez@gmail.com ![]() https://orcid.org/0000-0001-9446-820X
https://orcid.org/0000-0001-9446-820X
2 Profesor Investigador Asociado A. Departamento de Ecología y Conservación de la Biodiversidad. Laboratorio del medio físico, Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: olguin@cucsur.udg.mx ![]() https://orcid.org/0000-0002-6400-7039
https://orcid.org/0000-0002-6400-7039
3 Profesor Investigador Titular C. Departamento de Ecología y Conservación de la Biodiversidad. Laboratorio del medio físico, Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: rguevara@cucsur.udg.mx ![]() https://orcid.org/0000-0003-0940-7061
https://orcid.org/0000-0003-0940-7061
4 Profesor Investigador titular A. Departamento de Producción Agrícola. Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: oscar.mancilla@academicos.udg.mx ![]() https://orcid.org/0000-0003-4845-1188
https://orcid.org/0000-0003-4845-1188
5 Profesor Investigador Titular C. Departamento de Ecología y Conservación de la Biodiversidad. Laboratorio del medio físico, Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: cpalomera@cucsur.udg.mx ![]() https://orcid.org/0000-0001-5338-9177
https://orcid.org/0000-0001-5338-9177
6 Profesor Investigador Asociado C. Departamento de Ecología y Conservación de la Biodiversidad. Laboratorio de manejo forestal, Centro Universitario de la Costa Sur, Universidad de Guadalajara, Jalisco, México. Correo electrónico: Gerardo.cruz@cucsur.udg.mx ![]() https://orcid.org/0000-0002-8237-6217
https://orcid.org/0000-0002-8237-6217
Escuela de Ciencias Geográficas
Universidad Nacional, Campus Omar Dengo
Apartado postal: 86-3000. Heredia, Costa Rica
Teléfono: (506) 2562-3283
Correo electrónico revgeo@una.ac.cr