0298-19_34-1

El artículo presenta un estudio de casos sobre los significados que un grupo de profesores de matemáticas en formación inicial otorga al teorema de Pitágoras. Para esto, se enfatizó el análisis de uno de los organizadores del currículo: los modos de uso de un concepto matemático. Los participantes fueron 20 estudiantes de Enseñanza de la Matemática, provenientes de las 4 universidades públicas de Costa Rica donde se oferta esta carrera. La información se recolectó mediante el diseño y la aplicación de un cuestionario compuesto por 7 ítems tanto para el planteo como para la resolución de tareas sobre los usos del teorema de Pitágoras. Se destacan las respuestas dadas a 2 de esos ítems, vinculados a la fenomenología de un concepto matemático. Se utilizó uno de los componentes del análisis didáctico, el análisis de contenido, como técnica para examinar y caracterizar las situaciones junto con los contextos que ese grupo de estudiantes propone en el planteamiento y la resolución de tareas matemáticas enlazadas a la funcionalidad del teorema. Los resultados muestran que dicho teorema se concibe con el propósito de resolver tareas en situaciones matemáticas, basadas en el cálculo de longitudes; aunado a esto, se reconocen a) ciertas dificultades en los participantes para plantear asignaciones basadas en circunstancias distintas a un entorno matemático y b) que la calidad de las tareas propuesta es diversa.

Palabras clave: teorema de Pitágoras; modos de uso; situaciones y contextos; análisis de contenido; profesores de matemáticas en formación.

Abstract

This article presents a case study on the meanings that beginning students of mathematics teaching assign to the Pythagorean theorem. In this study, emphasis was placed on one of the most important elements used for structuring a curriculum: the ways in which students of mathematics teaching make use of a mathematical concept. Twenty (20) students of Mathematics Teaching from the four public universities of Costa Rica that offer this career participated in the study. A questionnaire was designed and applied for collecting information, which consisted of 7 items which presented and solved tasks based on the use of the Pythagorean theorem. Answers to two of these items stand out, which are associated with the phenomenology of a mathematical concept. Content analysis, one of the components of didactic analysis, was used to examine and characterize teaching situations, together with the contexts proposed by this group of students for the statement and solution of mathematics tasks associated with the theorem. The results show that this theorem was mainly seen as a tool for solving mathematical tasks related to the calculation of lengths. Additionally, participants experienced some difficulties in proposing tasks based on non-mathematical situations, and the quality of the tasks proposed varies.

Keywords: Pythagorean theorem; uses; situations and contexts; content analysis; training of beginning mathematics teachers.

Resumo

O artigo apresenta um estudo de casos sobre os significados que um grupo de professores de matemática na formação inicial outorga ao teorema de Pitágoras. Para isso, enfatizou-se a análise de um dos organizadores do currículo: os modos de usar um conceito matemático. Os participantes foram 20 estudantes de Ensino de Matemática, procedentes de 4 universidades públicas da Costa Rica, onde a carreira é oferecida. As informações foram coletadas por meio do desenho e aplicação de um questionário composto por 7 itens, tanto para a proposta quanto para a resolução de tarefas sobre os usos do teorema de Pitágoras. Destacamos as respostas dadas a 2 desses itens, ligados à fenomenologia de um conceito matemático. Utilizou-se um dos componentes da análise didática: a análise de conteúdo, como técnica para examinar e caracterizar as situações juntamente com os contextos que esse grupo de alunos propõe na abordagem e resolução de tarefas matemáticas vinculadas à funcionalidade do teorema. Os resultados mostram que este teorema é concebido com o propósito de resolver tarefas em situações matemáticas, baseado no cálculo de comprimentos; atado a isso, é reconhecido que a) há certas dificuldades nos participantes para propor tarefas baseadas em circunstâncias diferentes de um ambiente matemático e b) a qualidade das tarefas propostas é diversa.

Palavras-chaves: teorema de Pitágoras; modos de uso; situações e contextos; análise de conteúdo; professores de matemática em formação.

Introducción

En las agendas de investigación en educación matemática, sobresale el interés por el estudio de los significados atribuidos a conceptos matemáticos. Siguiendo a Rico, Lupiáñez, Marín y Gómez (2007), el análisis de contenido aporta al desarrollo de capacidades específicas que permiten organizar y priorizar el significado de dichos conceptos; además, insta a mejorar el proceso de aprendizaje de los estudiantes y estimula la reflexión en la labor docente (Marín, 2011). Asimismo, ese análisis analiza un contenido en particular y las relaciones de este con otros contenidos, contribuyendo así a centrarse en los más apropiados, según los objetivos de enseñanza, y a establecer un plan de acción o propuesta didáctica que beneficie tanto el proceso educativo como el aprendizaje significativo.

El significado de un concepto se conoce a partir de los 3 componentes del triángulo semántico, propuestos por Frege (1998): signo, sentido y referencia. En este marco, Rico (1997) aborda el significado de un concepto matemático, desde 3 organizadores del currículo: los sistemas de representación (el signo), que destacan los modos de expresión del concepto y sus propiedades; los modos de uso o fenomenología (el sentido), que comprenden las situaciones y contextos en los cuales se aplica el tópico matemático, y la estructura conceptual (la referencia), que toma en consideración conceptos, propiedades y relaciones entre conceptos (Rico, 2003; Rico y Fernández-Cano, 2013).

El creciente interés por el estudio del conocimiento matemático y didáctico manifestado por los profesores de matemática, más su desempeño como profesionales; las iniciativas de cambio curricular incidentes en los procesos formativos de estos docentes, y, desde una perspectiva matemática particular, la perpetuidad del teorema de Pitágoras en el currículo escolar, en el nivel global, la cual destaca su aporte histórico, así como su riqueza matemática y didáctica, han sido elementos que conducen a cuestiones sobre los significados que los profesores de matemática en formación inicial otorgan a ese teorema. Aunado a esto, ha tomado realce realizar una caracterización de los objetivos y las estrategias que proponen los profesores para la enseñanza y el aprendizaje del teorema, en el marco de su utilización en una diversidad de situaciones y contextos.

En este artículo, se enfoca el teorema de Pitágoras, como relación matemática, por su valor en el ámbito escolar y la matemática misma, y la importancia de sus aplicaciones en otras disciplinas. Este valor radica, además de su presencia en los planes de estudio de matemática y su conexión con una variedad de temas, en que constituye un recurso para incentivar la práctica deductiva de la matemática en el aula. Es un teorema con una valía cultural sobresaliente, cuya exposición pudo haber sido pionera en la historia de la demostración matemática y se ha constituido en la base para la promulgación de otros teoremas geométricos y trigonométricos (Strathern, 2014; Marín, 2011; González, 2008).

Con especificidad, se muestran los resultados de un estudio llevado a cabo para caracterizar los significados que un grupo de profesores de matemáticas, en formación inicial, en Costa Rica, otorgan al teorema de Pitágoras (Castillo, Chaverri-Hernández, Hernández y Vallejos, 2017), acentuando uno de los organizadores del currículo que permiten esta caracterización: los modos de uso de un concepto matemático (Rico, 1997). Es decir, se exponen los resultados vinculados al conocimiento matemático escolar sobre el teorema de Pitágoras, en términos de los fenómenos, entendidos como las situaciones y los contextos que expresan los profesores de matemáticas en formación inicial, al resolver 2 tareas matemáticas.

Antecedentes

El teorema de Pitágoras y su enseñanza han sido objeto de estudio en múltiples investigaciones, en el nivel internacional. A continuación, se destacan algunas de estas indagaciones.

Gavilán y Barroso (2001) resaltan el teorema de Pitágoras desde su importancia y el estudio de su demostración; los autores destacan el descubrimiento de fórmulas que permiten encontrar ternas para que las medidas de los catetos de un triángulo rectángulo, o de la hipotenusa y del cateto mayor, sean números consecutivos. Su planteamiento coincide con González (2008), quien recalca las diferentes demostraciones del teorema.

Dalcín (2007) establece que, posterior a los procesos de formación en educación secundaria, los estudiantes suelen olvidar el recíproco del teorema de Pitágoras o tienden a confundirlo con dicho teorema. Ruiz (2000) y Sutton (2012) enfatizan distintos aspectos sobre el teorema de Pitágoras que son relevantes para los estudiantes universitarios y cómo ellos comprenden algunos de los conceptos relacionados con este (como variable, pendiente, entre otros). Pinto (2012), mediante un estudio con profesores en formación inicial, identifica algunas dificultades asociadas al significado del teorema, sus fundamentos se basan en un uso inadecuado del lenguaje matemático, al momento de expresar el teorema.

Desde la perspectiva didáctica, Strathern (2014) centra los aportes de los pitagóricos en disciplinas como la astronomía y atribuye al teorema “el salto” de la matemática hacia una estructura de razonamiento deductivo. En la misma línea, De Brito (2010) evidencia la aplicabilidad del teorema de Pitágoras en otras ciencias y su importancia en la resolución de problemas. Garciadiego (2002) acentúa el hecho de que, cuando “se simplifica en didáctica”, puede ocasionarse una serie de conflictos conceptuales y cognitivos en los estudiantes; su tesis la ejemplifica con un análisis de la demostración del teorema, presentada en Los elementos de Euclides. Martínez (2000), Motta y Opazo (2012) plantean que las demostraciones del teorema y su enunciado constituyen un recurso importante para la enseñanza.

Otras investigaciones abordan la enseñanza del teorema de Pitágoras, por ejemplo, realzando la presentación de “actividades cognitivas” para su aprendizaje (Osorio, 2011). Meavilla (1989) afirma que los alumnos desconocen el significado del teorema, puesto que desvinculan la relación pitagórica (a2 = b2 + c2 o una particularización de esta) de la relación entre áreas o su ligazón con el triángulo rectángulo. Por su parte, en Costa Rica, Vargas y Gamboa (2013a) reconocen que existe una crisis en la enseñanza de la matemática en educación secundaria, particularmente, subrayan que la geometría es una de las áreas en las que se presentan mayores dificultades.

Aunado a esto, Barreto (2010) destaca deducciones del teorema, a partir de la noción de áreas; esto se propone como un recurso didáctico con base en el cual el estudiante podrá comprender, de mejor manera, la generalización del teorema. Peñafiel y Yun (2008) también consideran la relación entre áreas para exponer el teorema de Pitágoras, con el fin de que los educandos puedan identificar relaciones entre las áreas de figuras construidas sobre los lados de un triángulo rectángulo. Fernández (2015) realiza una propuesta didáctica basada en el teorema, mediante el análisis de libros de texto; el autor plantea varios problemas que destaquen su aplicación en la obtención de longitudes, la construcción de puzles pitagóricos, el uso de las TIC, el cálculo de áreas, problemas que involucran otras figuras planas y aplicaciones en la vida cotidiana; partiendo de su estudio, clasifica estos problemas en aritméticos, algebraicos, geométricos y tecnológicos.

Desde el marco del examen del teorema de Pitágoras, a partir del análisis de contenido matemático, Perry (2000) realiza una propuesta para abordarlo, basado en el análisis didáctico. Marín (2011) y Guardia, Montes, Páez, y Schmidt-Kortenbush (2009) elaboran unidades didácticas para tratar el teorema y distinguen, en el análisis fenomenológico, 3 situaciones referentes a longitudes, áreas y perpendicularidad, en las cuales se agrupan, generalmente, las tareas a las que debían responder los participantes en su estudio. En otras palabras, la clasificación de las situaciones es con base en si las tareas refieren a la medida de algún espacio métrico o distancia, comparación de áreas de figuras geométricas planas y análisis de perpendicularidad, respectivamente.

Marco teórico

Como parte de la delimitación teórica de esta investigación, se destacan diversas conceptualizaciones correspondientes al foco matemático y didáctico del estudio. En el primero, se presentan varias definiciones del teorema de Pitágoras. En el segundo, sobresale el análisis didáctico como marco general de la indagación. Se particulariza la categoría fenomenología o modos de uso del análisis de contenido, como componente del análisis didáctico. Estos se complementan con un abordaje de los planteamientos para el estudio del significado (o significados) de un concepto matemático.

Teorema de Pitágoras

El teorema de Pitágoras es conceptualizado de diferentes formas. A continuación, se muestran algunas de las definiciones presentes en diversas fuentes de información.

Perry (2000) plantea distintos enunciados del teorema, a partir de la consideración de 3 ópticas: áreas, medidas y números.

Áreas: el área del cuadrado de lado congruente con la hipotenusa de un triángulo rectángulo es igual que la suma de las áreas de los cuadrados de lados congruentes con los catetos de dicho triángulo.

Medidas: la medida del área del cuadrado de lado congruente con la hipotenusa de un triángulo rectángulo es igual que la suma de las medidas de las áreas de los cuadrados de lados congruentes con los catetos de dicho triángulo.

Números: el cuadrado (como potencia) de la medida de la longitud de la hipotenusa de un triángulo rectángulo es igual que la suma de los cuadrados de las medidas de las longitudes de los catetos de dicho triángulo (p. 154).

Por su parte, Barreto (2010) presenta 4 maneras para enunciar el teorema de Pitágoras, mostrando una extensión en la forma de interpretarlo.

1. “En todo triángulo rectángulo, el área del cuadrado construido sobre la longitud de la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre las longitudes de los catetos” (p. 72).

2. “En todo triángulo rectángulo, el área del triángulo equilátero construido sobre la longitud de la hipotenusa es igual a la suma de las áreas de los triángulos equiláteros construidos sobre las longitudes de los catetos” (p. 72).

3. “En todo triángulo rectángulo, el área de un semicírculo construido sobre la longitud de la hipotenusa es igual a la suma de las áreas de los semicírculos construidas sobre longitudes de los catetos” (p. 77).

4. “En todo triángulo rectángulo, el área de la lúnula construida sobre la longitud de la hipotenusa es igual a la suma de las áreas de las lúnulas construidas sobre longitudes de los catetos” (p. 78).

Tomando como base la obra Los elementos de Euclides, Joyce (1996) define el teorema en términos de las áreas de los cuadrados construidos sobre los lados de un triángulo rectángulo: “en los triángulos rectángulos el área del cuadrado construido sobre el lado opuesto al ángulo recto es igual a la suma de las áreas de los cuadrados construidos sobre los lados que comprenden el ángulo recto” (Traducción de los autores: “in right-angled triangles the square on the sides opposite the right angle equals the sum of the squares on the sides containing the right angle”) (párr. 1).

Otras definiciones o enunciados del teorema se han extraído de libros de texto elaborados para la educación secundaria en Costa Rica. Algunos de estos se describen a continuación.

“En un triángulo rectángulo, el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de las medidas de sus catetos” (Jiménez, 2005, p. 125).

“En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos” (Grupo Nación, 2011, p. 78).

“En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto” (MEP, 2012, p. 345) –esto se establece como una transcripción de la proposición 47 del libro I de Los elementos de Euclides–.

El teorema se concibe como algo más que un enunciado que admite un valor de verdad y que, por tanto, se puede demostrar. Constituye un objeto matemático, el cual permite conectar múltiples áreas de la matemática contempladas en el currículo escolar. Para efectos de esta investigación, se entiende el enunciado del teorema de Pitágoras de la siguiente manera: en un triángulo rectángulo, el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de las medidas de los otros 2 lados del triángulo (llamados catetos); considerando las diferentes áreas de la matemática en las que se puede definir o interpretar (Perry, 2000; Barreto, 2010).

Complementariamente, se adopta la propuesta de Perry (2000), en cuanto a que las diferentes formas de enunciar el teorema ponen de manifiesto las distintas temáticas con que este se relaciona. De tal manera, se pueden mostrar 2 conexiones del teorema: (a) con figuras geométricas planas, específicamente con triángulos, cuadriláteros, circunferencias y polígonos; y (b) con expresiones algebraicas, ya que, para implementarlo, interesa un dominio del concepto de variable, que se asigne una representación simbólico-algebraica a cada lado de un triángulo rectángulo, se resuelvan ecuaciones y se efectúen operaciones como la potenciación y la radicación, al igual que el manejo de las denominadas fórmulas notables.

Análisis didáctico

Desde un marco general, Castro (2015) apunta que el análisis didáctico se vincula al ámbito investigativo. Su planteamiento expresa que este análisis “se puede usar como metodología de investigación de orientación cuantitativa o cualitativa en una primera instancia, y como [fundamento para la] evaluación de la evaluación [de la actividad investigadora], en una segunda instancia” (p. 13). Esto considera que cada una de las fases del análisis didáctico se asocia a un proceso de análisis que posibilita orientar la parte metodológica en una investigación y, debido a su orden, estructura y característica cíclica, faculta recabar información, sintetizarla y evaluar la indagación.

El análisis didáctico constituye, entre otros aspectos, un organizador en el diseño de unidades didácticas, a través de los análisis parciales que lo componen (de contenido, cognitivo, de instrucción y de evaluación) y se presentan en forma cíclica e interrelacionada (Rico, 2003; Rico y Fernández-Cano, 2013; Rico y Moreno, 2016). Desde esta perspectiva, contribuye a fomentar competencias matemáticas en profesores y estudiantes –como objetivos a largo plazo–, por medio del desarrollo y la aplicación de las capacidades que se deben ver reflejadas en las tareas planificadas por los docentes.

Para esta investigación, se ha delimitado el campo de estudio a uno de los componentes del análisis didáctico: el análisis de contenido. Este presenta un esquema de 3 categorías para el examen de los significados de un concepto matemático; de estas, la fenomenología o modos de uso del concepto es la categoría que interesa.

Análisis de contenido matemático

El análisis de contenido organiza e identifica el significado de un concepto matemático, a partir del examen de su estructura conceptual, sus representaciones y su fenomenología (Rico, 2013). En particular, para este artículo se toma en cuenta únicamente el componente de fenomenología (los modos de uso), el cual considera que el significado de los conceptos matemáticos se muestra al presentar su conexión con la realidad, con los fenómenos.

La fenomenología refiere al estudio de los fenómenos, a la descripción de aquello que es notorio o aparece. En didáctica de la matemática, la fenomenología se concibe como una agrupación de fenómenos; esto difiere del análisis fenomenológico, que se entiende como la descripción de los fenómenos y su vínculo con el concepto en estudio (Segovia y Rico, 2001).

Siguiendo a Gómez (2007), la fenomenología es “un elemento constitutivo del significado de un concepto [que surge] de una visión funcional del currículo, en virtud de la cual los sentidos en los que se usa un término conceptual matemático también incluyen los fenómenos que sustentan el concepto” (p. 50). Desde la fenomenología, se destaca el otorgamiento de sentido práctico, al momento de establecer una relación entre una estructura matemática y los fenómenos que se asocian a esta (Gómez y Cañadas, 2011).

Particularmente, los fenómenos se conciben como “toda manifestación que se hace presente a la consciencia de un sujeto y aparece como objeto de su percepción” (Real Academia Española, 2019). En educación matemática, es común concebir los fenómenos como aquellas situaciones o problemas en los que se enmarca o se manifiesta el uso o la aplicación de un concepto matemático.

Para este estudio, se adopta la organización de los fenómenos, con base en 2 criterios: contextos y situaciones.

Contextos matemáticos. Generalmente, los contextos responden a la pregunta “¿para qué se utilizan estas nociones?, refieren al modo en que se usan los conceptos, en una o varias situaciones” (Rico, Marín, Lupiáñez, y Gómez, 2008, p. 12). La idea de contexto se emplea aquí para referir a un grupo de fenómenos que comparten características estructurales.

Situaciones. Una situación “viene dada por una referencia al medio (natural, cultural, científico y social) en el cual se sitúan tareas y cuestiones matemáticas que pueden encontrar los ciudadanos, que se proponen a los estudiantes y que centran su trabajo” (Rico, Lupiáñez, Marín y Gómez, 2007, p. 11).

En cuanto a la concepción de modo de uso, la RAE (2019) define uso como la acción de “hacer servir una cosa para algo”. Por su parte, el término modo, se presenta como el “procedimiento o conjunto de procedimientos para realizar una acción”; se entiende, además, como la “forma especial que puede adoptar un fenómeno”. Los modos de uso expresan, entonces, las maneras, formas o procedimientos en que un concepto matemático sirve o es útil para un determinado propósito; es decir, dan sentido al concepto. Así, se enlazan las nociones de modos de uso y fenomenología, consideradas en este trabajo.

Significado de un concepto matemático

Anteriormente, se ha referido al triángulo semántico de Frege (1998) como fundamento para el estudio del significado de un concepto. Sin embargo, se adopta la propuesta de Rico (1997), con el propósito de establecer el significado de un concepto matemático, mediante 3 organizadores del currículo: estructura conceptual, sistemas de representación y fenómenos (figura 1).

Comprender un concepto matemático es, por tanto, dotarlo de significado. Esto implica conocer su definición, la variedad de representaciones y los distintos modos para dar sentido al concepto ‘mostrar su utilidad en situaciones y contextos diversos’. Estos componentes del triángulo semántico corresponden a los elementos del análisis de contenido matemático (Rico, 2013).

En adición, el análisis de contenido permite reconocer y organizar el significado de un objeto matemático, al mismo tiempo que lleva a disponer de un referente para identificar los dominios del conocimiento matemático del profesor.

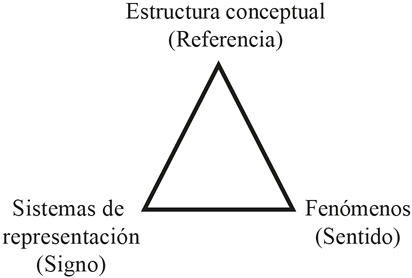
Figura 1.

Dimensiones del significado de un concepto matemático escolar (Gómez, 2007). Extraído de: Desarrollo del conocimiento didáctico en un plan de formación inicial de profesores de matemáticas de secundaria. Universidad de Granada, España.

En este sentido, Rojas (2014) establece, mediante una serie de indicadores, un vínculo entre los dominios del conocimiento matemático y los componentes del análisis de contenido matemático. Sin embargo, estos indicadores se plantean a partir del concepto de fracción que, para el propósito de este estudio, fueron adaptados al teorema de Pitágoras. Los indicadores empleados por Castillo, Chaverri-Hernández, Hernández y Vallejos (2017), según los dominios del conocimiento del contenido matemático de Carrillo, Contreras y Flores (2013) para el análisis fenomenológico, se muestran en la tabla 1.

Tabla 1

Fenomenología: indicadores del conocimiento en el análisis de contenido matemático

Conocimiento

Indicadores

Conocimiento de los temas

Conocer variedad de significados del teorema, asociados a distintos modos de actuación.

Reconocer distintas formas en que se explicita la relación pitagórica en la matemática.

Identificar variedad de situaciones y contextos de las tareas que involucran al teorema de Pitágoras.

Conocimiento de la estructura matemática

Variedad de significados y relaciones con otros conceptos matemáticos, que permiten asociar el teorema a distintos modos de uso.

Nota: Fuente propia de la investigación.

Cabe resaltar que un tercer indicador, “Conocimiento de la práctica matemática”, fue descartado, debido a que los participantes en la investigación eran profesores de formación inicial; es decir, no habían ejercido profesionalmente como docentes.

Marco metodológico

El estudio llevado a cabo se enmarca en las investigaciones en didáctica de la matemática; es una investigación cualitativo-descriptiva basada en el estudio de casos. Con su desarrollo, se describe el conocimiento matemático sobre el teorema de Pitágoras que expresan los profesores de matemáticas en formación, desde el examen de los fenómenos manifestados.

En Costa Rica, el trabajo es una iniciativa para la indagación sobre significados de conceptos matemáticos, en la línea de investigación sobre la formación de profesores.

Sujetos participantes

Debido a su disponibilidad, la muestra de profesores en formación inicial considerada fue intencional. Participaron 20 estudiantes seleccionados de las 4 universidades estatales del país que ofrecen la carrera Enseñanza de la Matemática: la Universidad de Costa Rica, la Universidad Nacional, el Instituto Tecnológico de Costa Rica y la Universidad Estatal a Distancia. Se seleccionaron 5 estudiantes de cada institución, tomando en cuenta, además de su disponibilidad, otros criterios de selección como: nivel académico, referencia y experiencia.

El nivel académico considera los cursos aprobados por los participantes. Luego de una revisión de los programas de estudio de las 4 universidades de procedencia, se determinó que los profesores debían estar, al menos, en el segundo año de carrera, ya que se requería tener aprobados los cursos sobre geometría euclídea que se imparten en los 3 primeros semestres de los planes de estudio. Este criterio se considera relevante, debido a que, generalmente, en dichos cursos se aborda el teorema de Pitágoras y su recíproco, desde un punto de vista formal (demostrativo); lo que supone una amplitud del conocimiento de los docentes en formación, respecto al objeto de interés de esta investigación.

En cuanto al criterio de referencia, destaca la recomendación del(de los) docente(s) formador(es) que imparte(n) los cursos de geometría euclídea en cada universidad. Se consideró una lista de al menos 10 estudiantes por universidad, para garantizar la participación de los 5 requeridos. Los profesores de las universidades tienen un mayor contacto con los estudiantes y pueden referirse a ellos como posibles participantes en la recolección de datos.

El criterio de experiencia remite a la selección de participantes, según el ejercicio de su práctica. Es decir, se seleccionaron docentes en formación sin desempeño profesional. Lo anterior, considerando que el conocimiento del profesor es directamente afectado por su práctica y esta es una variable ajena al interés de la investigación.

Instrumento de recolección de datos

La información tratada se recolectó mediante el diseño, la elaboración y la aplicación de un cuestionario de respuesta abierta. Este se efectuó a partir de una adaptación de otros instrumentos facilitados por investigadores del Grupo de Investigación Pensamiento Numérico, del Departamento de Didáctica de la Matemática de la Universidad de Granada, sobre el estudio de significados de conceptos matemáticos. Los ajustes consideraron su delimitación al contexto educativo costarricense y al teorema de Pitágoras como objeto de la investigación.

El instrumento fue validado mediante su aplicación –una prueba piloto– a 7 estudiantes de la Universidad de Costa Rica. Dadas las respuestas de estos, se realizaron modificaciones, para garantizar la comprensión adecuada del enunciado de cada cuestión. Asimismo, el cuestionario se sometió a juicio de 2 expertos internacionales, quienes llevaron a cabo una revisión y emitieron recomendaciones en cuanto al propósito de los enunciados.

Los ítems del cuestionario se formularon con el fin de obtener información sobre la estructura conceptual, los sistemas de representación y aquellos aspectos relativos a la fenomenología que los participantes manifiestan sobre el Teorema de Pitágoras. Luego del proceso de validación y de la incorporación de modificaciones, los ítems correspondientes a la fenomenología fueron dos, enumerados en el cuestionario como ítem ٦ e ítem ٧. La información recabada a parir de estos dos ítems constituye el fundamento del análisis presentado en este trabajo. Los ítems son los siguientes.

Ítem 6. Plantee detalladamente al menos cuatro situaciones en las que es aplicable el Teorema de Pitágoras.

Con esta cuestión se pretendió identificar situaciones en las que los docentes en formación inicial consideraban útil y aplicable el teorema (solo debían mencionarlas).

Ítem 7. Enuncie dos problemas distintos cuya resolución implique el uso del Teorema de Pitágoras. Resuélvalos.

Este ítem pretendía evidenciar situaciones y contextos en los que los participantes aplican dicho teorema y la manera en que dan respuesta.

Organización de la información

La información recabada se organizó mediante categorías, subcategorías y unidades de análisis; construidas con base en el análisis de contenido matemático, indicadores del conocimiento matemático (Rojas, 2014), y las respuestas en los cuestionarios.

Para este estudio, la categoría corresponde a la componente fenomenología del análisis de contenido matemático. Las subcategorías responden a aspectos relacionados con esta categoría: tipos de situaciones, contextos para el cálculo matemático y calidad, esta última se construye como resultado de la investigación, es una subcategoría emergente. Las unidades de análisis refieren a los elementos específicos de cada subcategoría a partir de las respuestas obtenidas.

Categoría: Fenomenología.

1.Subcategoría: Tipos de situaciones. Comprende diferentes situaciones en las que es aplicable el Teorema de Pitágoras.

0.1. Matemático (SM). Comprende situaciones donde la solución es de un interés matemático únicamente.

0.2. Natural (SN). Establece situaciones que involucran fenómenos físico-naturales o elementos vinculados a la naturaleza.

0.3. Social (SS). Establece situaciones con objetos propios del hogar, la escuela o grupos sociales, así como actividades recreativas.

0.4. Científico-Técnica (SCT). Plantea situaciones vinculados a objetos de actividades científicas y técnicas.

0.5. Otras (OS). Menciona situaciones que no son clasificables en alguno de los criterios anteriores.

2.Subcategoría. Cálculo matemático. Comprende los contextos de las operaciones o propiedades aritméticas involucradas en las situaciones presentadas.

2.1. Contexto longitud (CL). Presenta situaciones que requieren la aplicación del Teorema de Pitágoras para el cálculo de longitudes únicamente.

2.2. Contexto área (CA). Plantea situaciones que requieren la aplicación del Teorema de Pitágoras para calcular longitudes necesarias para determinar áreas.

2.3. Contexto volumen (CV). Plantea situaciones que requieren la aplicación del Teorema de Pitágoras para calcular longitudes necesarias para determinar volúmenes.

2.4. Contexto trigonometría (CT). Plantea situaciones que requieren la aplicación del Teorema de Pitágoras para calcular longitudes necesarias para determinar el valor de razones trigonométricas o bien deducir identidades trigonométricas.

2.5. Contexto recíproco del teorema (RCM). Las situaciones propuestas requieren la aplicación del reciproco del Teorema de Pitágoras para determinar si tres longitudes corresponden a las medidas de los lados de un triángulo rectángulo.

2.6. Otros (O). Establece otros contextos que requieren el Teorema de Pitágoras en el cálculo matemático.

3.Calidad de la situación. Expresa situaciones con coherencia lógica matemática; por ejemplo, las medidas de los elementos presentes en la situación son posibles matemáticamente hablando. Estas situaciones están apegadas a la realidad y muestran un uso adecuado de términos.

3.1. Alta. Las situaciones planteadas poseen coherencia lógica matemática y están apegadas a la realidad

3.2. Media. Las situaciones planteadas poseen coherencia lógica matemática o están apegadas a la realidad.

3.3. Baja. Las situaciones planteadas no poseen coherencia lógica matemática ni están apegadas a la realidad.

Las situaciones matemáticas (exclusivas) se clasificaron con niveles Alta o Baja; otorgando alta cuando las situaciones se expresan con coherencia lógica matemática, y baja en el caso contrario, por ejemplo, cuando se omiten propiedades o características básicas de las figuras geométricas utilizadas.

Análisis y resultados

Primeramente, se destacan los datos vinculados a las situaciones y los contextos manifestados por los profesores de matemática en formación inicial participantes; es decir, la diversidad de usos que estos proponen para mostrar la aplicabilidad del Teorema de Pitágoras. Analizadas las respuestas de los ítems 6 y 7, se estableció una evaluación de la calidad de las situaciones, a partir de la coherencia lógica matemática y su vínculo con la realidad.

Situaciones

Para el análisis llevado a cabo sobre los usos del teorema se consideraron cinco situaciones y seis contextos. Los resultados sobre las situaciones se muestran en la tabla 2.

Tabla 2

Situaciones consideradas para las respuestas a los ítems 6 y 7

Ítem	Situaciones
Ítem	SM	SN	SS	SCT	OS
Ítem 6	19	3	3	7	2
Ítem ٧	18	0	7	8	0

Nota. Fuente propia de la investigación. SM=situación matemática; SN=situación natural; SS=situación social; SCT=situación científico-técnica; OS=otra situación.

Como se aprecia, la mayoría de las situaciones mostradas en las respuestas a los ítems 6 y 7 son de carácter matemático, lo que se interpreta como una carencia de propuestas vinculadas a situaciones distintas a las matemáticas, es decir aquellas que se apeguen a la cotidianidad. Se destaca que, cuando los profesores deben plantear y resolver tareas que utilicen el Teorema de Pitágoras, la diversidad de las situaciones disminuye: las respuestas para el ítem 7 excluyen las situaciones naturales o las de otro tipo.

Particularmente, en lo que sigue se destaca la diversidad de situaciones mostradas en las producciones de los profesores para el ítem 7, debido a que en este ítem se requería la aplicación del Teorema de Pitágoras.

Situaciones Matemáticas

Los problemas (tareas) correspondientes a situaciones matemáticas respondieron en su mayoría a una caracterización de figuras geométricas; por ejemplo, el establecimiento de las longitudes de segmentos y el cálculo de perímetros, áreas o volúmenes. La mayoría se vinculan a figuras planas y en menor medida a sólidos geométricos. Un ejemplo de una situación matemática se muestra en la figura 2.

Figura 2.

Ejemplo de situación matemática. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Aquí se acentúa el empleo del Teorema de Pitágoras para determinar la longitud de un segmento (altura) en una figura plana (triángulo equilátero). Además, se reconoce como un caso poco convencional pues se debe averiguar la medida de un cateto en vez de la medida de la hipotenusa.

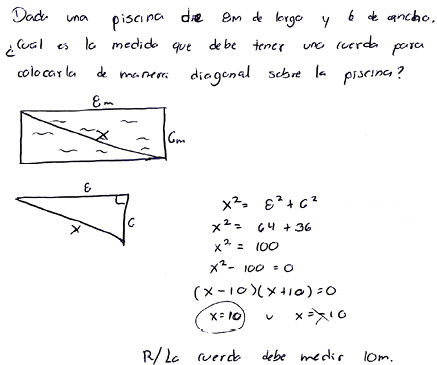
Figura 3.

Ejemplo de situación social. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Situaciones Sociales

Dentro de las situaciones sociales identificadas se encontraron fenómenos referentes al cálculo de la longitud de objetos como cables y cuerdas; ejemplificado con piscinas o teleféricos (ver figura 3). No obstante, la situación en la que se presenta la tarea carece de sentido, ya que no se identifica el propósito de colocar una cuerda en diagonal; es decir, no hay un problema o una intensión real explícita referida a su ubicación –de la cuerda–. Otros aportes refieren al cálculo del desplazamiento (recorrido) de una persona o un automóvil.

Situaciones científico-técnicas

Estas situaciones se identificaron en fenómenos que destacaban la longitud de objetos a partir de mediciones técnicas, como el largo de escaleras apoyadas sobre muros o edificios, la altura de un faro, la cantidad de gradas (o escalones) que caben en un espacio, la distancia entre dos objetos y la medida del lado o la diagonal de un terreno, o el perímetro de terrenos con formas geométricas. Un ejemplo se muestra en la figura 4.

Figura 4. Ejemplo de tareas en una situación científico-técnica. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Contextos

Los contextos identificados en las situaciones se clasificaron como respuesta a la pregunta ¿para qué se utiliza el teorema de Pitágoras? (Rico et al, 2008). Dentro de estos contextos destacan el cálculo de la longitud y el área en figuras geométricas planas, así como el cálculo del volumen en sólidos geométricos. La tabla 3 presenta los datos sobre los contextos identificados en las respuestas a los ítems 6 y 7.

Tabla 3

Contextos considerados para las respuestas a los ítems 6 y 7

Ítem	Contextos
Ítem	CL	CA	CV	CT	RCM	O
Ítem 6	19	6	3	2	2	3
Ítem 7	18	4	1	0	0	1

Nota. Fuente propia de la investigación. CL=contexto longitud; CA=contexto área; CV=contexto volumen; CT=contexto trigonometría; RCM= contexto recíproco del teorema, O=otro contexto.

De acuerdo con estos resultados, los docentes participantes consideran una mayor cantidad de contextos cuando plantean una tarea (ítem 6) –al igual que para las situaciones– que cuando se requiere de un enunciado y su solución (ítem 7); es decir, esta diversidad de contextos se reconoce cuando solo deben mencionar los modos de uso del teorema.

Al igual que para las situaciones, en lo que sigue se destacan las especificidades de los contextos reconocidos en el ítem 7.

Contexto longitud

Dentro de este contexto se busca determinar diferentes longitudes asociadas, principalmente, a figuras planas: el perímetro de polígonos regulares e irregulares, las diagonales de cuadrados y rectángulos, los lados de un triángulo.

También se destaca el cálculo de longitudes en figuras tridimensionales: la diagonal de un cubo, la arista de una pirámide, la altura y generatriz de un cono y la distancia del centro de una esfera a su superficie. Además, se evidencian fenómenos que presentan el cálculo de distancias entre dos puntos en el plano cartesiano (dos dimensiones) y la distancia mínima entre un punto y un segmento (figura 5).

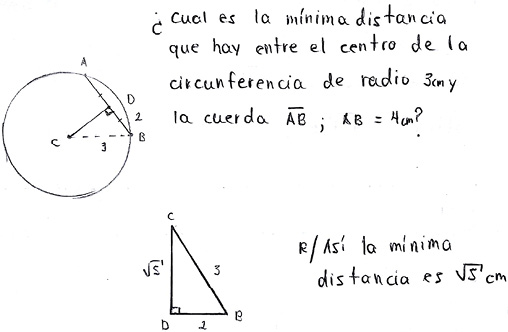
Figura 5.

Situación matemática - Contexto longitud. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Contexto área

En este contexto se contemplan fenómenos sobre el cálculo de áreas de figuras planas como polígonos regulares e irregulares –mayormente para triángulos– y en figuras tridimensionales, específicamente para el área lateral de un cono (ver figuras 6 y 7).

Figura 6.

Ejemplo de tarea de contexto área, en una situación matemática tridimensional. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

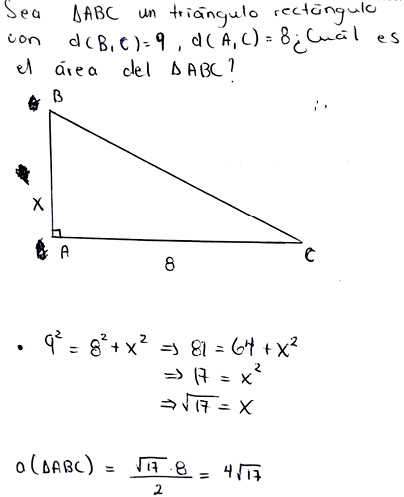
Figura 7.

Ejemplo de tarea de contexto área, en una situación matemática plana. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Los contextos área y volumen incluyen pocos fenómenos; para el contexto de volumen solo se refiere a su cálculo particularizado a una caja de base cuadrada, que se modeló con un cubo sin indicar la medida de su diagonal. La figura 8 presenta este caso.

Figura 8.

Situación matemática - Contexto volumen. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Fenómenos en cada contexto y situación

A partir de las respuestas de los participantes al ítem 7, se presentan los fenómenos identificados que vinculan contextos y situaciones, en los que se requiere la aplicación del Teorema de Pitágoras (tabla 4).

Se observa que las situaciones matemáticas se encuentran distribuidas en una mayor cantidad de contextos, de los cuales destaca el contexto longitud. Además, puede apreciarse que las situaciones de tipo social y científico-técnicas abarcan únicamente el contexto longitud, donde refieren principalmente al cálculo de la medida de los lados de un triángulo rectángulo, un rectángulo o un cuadrado.

Por otra parte, a partir del análisis del ítem 6, los participantes mencionan algunas tareas en las que puede ser aplicable el Teorema de Pitágoras; esto complementa la información de la tabla anterior. La tabla 5 presenta los fenómenos identificados en cada contexto según el tipo de situación.

Tabla 4

Fenómenos en cada contexto según el tipo de situación en el ítem 7

Contextos	Fenómenos
Situaciones científico-técnicas
Longitud	Cálculo de la longitud de una escalera apoyada en una pared Cálculo de la longitud de una escalera apoyada en la cumbre de un edificio Cálculo de la distancia de una persona al punto más alto de un poste Cálculo de la medida de la diagonal de un terreno cuadrado Cálculo de la medida del lado de un terreno triangular Cálculo de la medida de la altura de un faro Cálculo de la cantidad de gradas que debe tener una escalera Cercar un terreno cuadrado
Situaciones matemáticas
Volumen	Cálculo de volumen de una caja cuadrada
Área	Cálculo del área lateral de un cono Cálculo del área e un triángulo rectángulo Cálculo del área de un trapecio isósceles Cálculo del área de un polígono irregular
Longitud	Cálculo de la diagonal de un cuadrado y un cubo Cálculo del perímetro de un polígono irregular Cálculo del cateto de un triángulo Cálculo de la hipotenusa Cálculo de la distancia entre el centro de una circunferencia y una cuerda Calcular la generatriz de un tronco de cono Cálculo de la longitud de un segmento Cálculo de la altura de un triángulo equilátero Cálculo de la distancia entre el centro de una esfera y un corte de esta Calcular la altura de un cono Segmentos en una pirámide
Otros	Determinar la forma geométrica de un número complejo
Situaciones sociales
Longitud	Calcular la distancia/desplazamiento recorrida/o por un automóvil/ persona Cálculo de la medida de una cuerda colocada diagonalmente en una piscina Cálculo de la medida del cable de un teleférico

Nota. Fuente propia de la investigación.

Tabla 5

Fenómenos en cada contexto según el tipo de situaciones en el ítem 6

Contextos	Fenómenos
Situaciones matemáticas
Volumen	Cálculo de volumen de figuras tridimensionales (cono)
Área	Cálculo del área de figuras planas (rombo, polígonos regulares, cuadrilátero)
Longitud	Cálculo de la distancia entre dos puntos en el plano cartesiano Cálculo de la apotema/arista/altura de una pirámide Calcular la medida de la diagonal de un prisma / rectángulo / cuadrilátero Cálculo del perímetro de una figura plana /cuadrilátero Cálculo de la distancia mínima entre dos puntos Determinar la medida de los lados de un triángulo isósceles / rectángulo
Trigonometría	Obtener las razones trigonométricas Deducción de identidades trigonométricas
Recíproco	Dados tres lados de un triángulo, halle el ángulo recto Dados tres lados de un triángulo, verifique si se cumple el Teorema de Pitágoras
Otro	Encontrar un vector resultante
Situaciones naturales
Longitud	Cálculo de la distancia de la sombra proyectada por un árbol Cálculo de la altura de un árbol
Situaciones sociales
Longitud	Cálculo de las medidas de los lados de un papalote Determinar qué camino es más corto entre dos ciudades
Situaciones científicas-técnicas
Longitud	Cálculo de la longitud de una rampa Cálculo de la altura de un edificio Cálculo de las dimensiones de una ventana
Área	Cálculo del área de un terreno triangular
Recíproco	Verificar la perpendicularidad de construcciones a nivel del suelo
Otras situaciones
Longitud	Determinar un cambio de posición con respecto al tiempo
Otro	Determinar, en programación, la cantidad ternas pitagóricas que se encuentran en un intervalo

Nota. Fuente propia de la investigación.

En la tabla 5 se muestran situaciones y contextos identificados en el ítem 6, que no se contemplaron como parte de la resolución del ítem 7, como lo son las situaciones naturales que abordan el cálculo de longitudes y los contextos de trigonometría, el recíproco del teorema y otros, donde el uso del teorema difiere del empleado en los demás contextos porque se requiere de deducciones y verificaciones; es decir, en estos no se reduce el teorema únicamente al cálculo de una medida.

En síntesis, a partir de una combinación de las producciones de los informantes a los ítems 6 y 7 se obtienen los resultados que se presentan en la tabla 6.

Tabla 6

Situaciones asociadas a cada contexto a partir de las soluciones a los ítems 6 y 7

Contexto	Situación
Contexto	Matemática	Natural	Social	Científico-técnica
Longitud
Área
Volumen
Trigonometría
Recíproco del teorema
Otro

Nota. Fuente propia de la investigación. =Se identificó un fenómeno en el contexto y situación; = No se identificó un fenómeno en dicho contexto y situación.

Como se aprecia, los fenómenos identificados se vinculan a situaciones matemáticas en todos los contextos, con la particularidad de que el contexto de longitud es el único presente en todas las situaciones.

Calidad de la situación

Para analizar la calidad de las situaciones se definieron tres unidades o niveles de calidad: alta, media y baja; estos se determinaron de acuerdo a la coherencia lógica-matemática y el vínculo de la situación con la realidad. Dado que las situaciones matemáticas no contemplan el apego a la realidad, se decidió analizar la presencia o ausencia de coherencia lógica matemática en estas situaciones, de esta forma se establecieron solo dos niveles de calidad: alta y baja. La tabla 7 expone la calidad de las situaciones del ítem 7.

Tabla 7

Frecuencia absoluta de situaciones por calidad según tipo de situaciones

Tipo de situación	Calidad Alta	Calidad Media	Calidad Baja
Matemáticas	16	-	5
Sociales y científico-técnicas	7	6	5
Total	23	6	10

Nota. Fuente propia de la investigación.

Cabe indicar que una de las situaciones no fue considerada para el análisis de la calidad de la situación, debido a que carecía de enunciado.

Entre los aspectos utilizados para atribuir una baja calidad a las situaciones matemáticas se encuentra la utilización del término distancia para hallar la medida de un lado de un triángulo; con este, por ejemplo, se identificaron enunciados como: “¿cuál es la distancia de la hipotenusa?”. También –en algunos casos– se solicitaba el área lateral de un cono o su altura, sin especificar si este correspondía a un cono circular recto. Un ejemplo de esto se muestra con la figura 9, en la cual tampoco se establece que el triángulo es rectángulo.

En cuanto a las situaciones sociales y científico-técnicas, que se clasificaron de calidad media, destaca la falta de claridad en su contextualización. Por ejemplo, la figura 10 muestra una situación en la que se combinan elementos de la realidad (muros) con elementos matemáticos (círculos); las demás muestran inconsistencias en la redacción del enunciado y en las dimensiones asignadas a los elementos involucrados de la vida real, como considerar un edificio con una altura de 3 metros.

Figura 9. Ejemplo de situación matemática con calidad baja. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

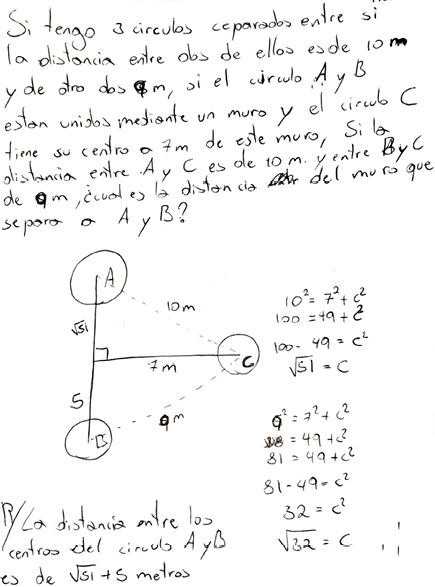
Figura 10. Ejemplo de situación cientifico-técnica con calidad media. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Figura 11. Ejemplo de situación social con calidad baja. Extraído de: Solución de uno de los informantes al ítem 7 del cuestionario.

Por otro lado, la calidad baja de estas situaciones fue atribuida a la existencia de ambigüedades en la redacción de los enunciados; por ejemplo, en el enunciado mostrado en la figura 11 se utiliza el término “distancia” para referirse al “desplazamiento” de un automóvil, además los datos o la información suministrada no coincide con el diagrama o el dibujo brindado.

Los resultados que se han destacado sustentan las afirmaciones que se muestran en el apartado de conclusiones. Con estas se caracteriza la manera en que este grupo de profesores de matemática en formación inicial tratan el uso del Teorema de Pitágoras a través del estudio de los fenómenos, las situaciones y contextos manifestados.

Conclusiones

El estudio permite concluir que los profesores en formación participantes muestran modos de uso diversos, desde su organización como contextos y situaciones, a la hora de plantear tareas, en cuya resolución es aplicable el Teorema de Pitágoras. Particularmente esta diversidad de usos se da cuando el planteamiento no incluye la resolución de la tarea o un mayor detalle de estas; es decir, el enunciado de tareas, por parte de esta población, se aborda desde la contextualización de la tarea, que en la actualidad es promovida para la enseñanza de las matemáticas en la Educación General Básica en Costa Rica (Educación Primaria completa, tres primeros años de la Educación Secundaria). En este sentido se reconoce una clarificación del entorno en el enunciado de las tareas que le otorga un grado de importancia en el proceso de planificación de estas. Cabe señalar que el planteo de problemas o tareas son fundamentales para la asimilación o aprendizaje significativo de un contenido; incluso, la formulación de un problema puede ser más importante que su resolución (Einstein e Infeld, 1986).

En este caso específico, la mayoría de las tareas mostradas se enmarcan en situaciones matemáticas (desvinculadas de otro tipo de situaciones de tipo cotidiano) y corresponden al contexto para el cálculo de longitudes, donde el uso del teorema se orienta principalmente al cálculo de longitudes en figuras en el plano. Contrariamente a los planteado Barreto (2010), Peñafiel y Yun (2008), Fernández (2015) y Perry (2000) quienes proponen el estudio del Teorema de Pitágoras a partir de áreas, para facilitar su aprendizaje.

El contexto de cálculo de longitudes fue el segundo con mayor presencia en las respuestas de los profesores en formación inicial (ver tabla 3), a pesar de que su frecuencia es “muy baja” en las respuestas para los dos ítems. Esta particularidad coincide con los planteamientos de Marín (2011) y Guardia et al. (2009), que destacan la tendencia de asociar la aplicabilidad del Teorema de Pitágoras en contextos referentes al cálculo de longitudes (en primera instancia) y áreas.

Los resultados del estudio aportan a la tesis de Dalcín (2007), quien establece que el recíproco del Teorema de Pitágoras es generalmente olvidado por los estudiantes una vez que han concluido sus estudios en educación secundaria. Las evidencias mostradas destacan la poca frecuencia con que se utiliza este recíproco, como contexto para la resolución de determinadas situaciones o problemas.

En cuanto a la calidad de las situaciones, estas muestran un nivel alto cuando las situaciones consideradas por los participantes fueron matemáticas, en estos casos las medidas de los elementos involucrados son posibles y el uso del lenguaje o términos es adecuado; es decir, en estas se muestra una coherencia lógica matemática. Cuando las situaciones corresponden a otros tipos –es decir, no corresponden a la categoría matemáticas– su calidad se encuentra entre los niveles medio o bajo, debido a que poseen deficiencias en los elementos que caracterizan la coherencia lógica matemática descrita.

Cuando las situaciones tratadas son matemáticas los profesores participantes involucran todos los tipos de contextos definidos para el estudio (longitud, área, volumen, trigonometría, recíproco del teorema, otro). Esta particularidad no se reconoce con las demás situaciones, a pesar de que las aplicaciones del teorema son innumerables en situaciones cotidianas (Marín, 2011). Esto, junto al hecho de que algunas de estas situaciones no se apegan a la realidad o bien se presentan haciendo un uso incorrecto de conceptos matemáticos, puede evidenciar la presencia de dificultades cuando se plantean tareas en situaciones no matemáticas que involucren el Teorema de Pitágoras.

Las evidencias del estudio conducen a considerar el análisis de contenido como una herramienta poderosa para el estudio de la planificación escolar, puesto que permite el fomento de capacidades para organizar y priorizar significados de un concepto matemático (Rico et al, 2007), acentuando, en este caso, su uso y aplicabilidad. Si solo se ejercita al estudiante en la resolución de operaciones rutinarias –particularmente, sin establecer conexiones entre conceptos y su aplicabilidad– se acabará su interés y esto impedirá su desarrollo intelectual, por lo que se debe seleccionar cuáles y cómo se abordan ciertos contenidos en el aula (Polya, 1989). Los docentes deben contar con conocimientos variados para guiar a sus estudiantes durante el proceso de aprendizaje (Vargas y Gamboa, 2013b). Esta variedad de sapiencia puede constituirse, particularmente, a partir de la implementación del análisis de contenido para el estudio de un concepto matemático.

El abordaje del Teorema de Pitágoras, como contenido escolar, debe enfatizar su aplicabilidad “real” en distintas y diversas situaciones de la cotidianeidad, de manera que se consideren una mayor variedad de contextos y se explicite la riqueza conceptual que engloba este teorema en las matemáticas escolares.

Bibliografía

Barreto, J. C. (2010). Deducción y extensión más general del Teorema de Pitágoras. Números, 75, 71-87. Recuperado de http://www.sinewton.org/numeros/numeros/75/Articulos_01.pdf

Carrillo, J.; Contreras, L. y Flores, P. (2013). Un modelo de conocimiento especializado del profesor de matemáticas. En L. Rico, M. Cañadas, J. Gutiérrez, M. Molina e I. Segovia (Eds.). Investigación en Didáctica de la Matemática. Libro homenaje a Encarnación Castro (pp. 193-200). Granada, España: Comares.

Castillo, M.; Chaverri-Hernández, J.; Hernández, K. y Vallejos, A. D. (2017). Estudio de los significados atribuidos al Teorema de Pitágoras que manifiestan profesores de matemática en formación inicial en Costa Rica (Tesis de licenciatura). San José, Costa Rica.

Castro, E. (2015). Significados de las fracciones en las matemáticas escolares y formación inicial de maestros (Tesis de doctorado). Universidad de Granada, España. Recuperado de https://hera.ugr.es/tesisugr/24939493.pdf

Dalcín, M. (2007). Recíproco de Pitágoras. Sociedad Argentina de Educación Matemática. Documento en línea. Recuperado de http://www.soarem.org.ar/Documentos/34%20Dalcin.pdf

De Brito, A. (2010). Teorema de Pitágoras: qual a sua importância para o ensino das ciências da natureza? (Tesis de Maestría). Universidad do Grande Rio, Brasil.

Einstein, A. & Infeld, L. (1986). La evolución de la física. Barcelona, España: Salvat Editores, S.A. Recuperado de http://www.fisicamente.net/FISICA/Evolucion_Fisica.pdf

Fernández, D. (2015). Teorema de Pitágoras: una propuesta didáctica para 2º de ESO (Tesis de maestría). Universidad Zaragoza, España.

Frege, G. (1998). Comentarios sobre sentido y referencia. En L. M. Valdés (Ed.), Ensayos de semántica y filosofía de la lógica (pp. 84-111). Madrid, España: Tecnos.

Garciadiego, A. (2002). El Teorema de Pitágoras como paradigma de la enseñanza de la geometría plana: simplificar no siempre simplifica. Revista latinoamericana de Investigación en Matemática Educativa, 5, 251-270.

Gavilán, J., & Barroso, R. (2001). Diversas perspectivas del Teorema de Pitágoras. Épsilon, ٥٠, 283-292.

Gómez, P. (2007). Desarrollo del conocimiento didáctico en un plan de formación inicial de profesores de matemáticas de secundaria (Tesis de doctorado). Universidad de Granada, España. Recuperado de http://funes.uniandes.edu.co/444/1/Gomez2007Desarrollo.pdf

Gómez, P. y Cañadas, M. (2011). La fenomenología en la formación de profesores de matemáticas. Voces y Silencios: Revista Latinoamericana de Educación, 2, 78-89. Recuperado de https://revistas.uniandes.edu.co/doi/abs/10.18175/vys2.especial.2011.05

González, P. (2008). El teorema llamado de Pitágoras. Una historia geométrica de 4.000 años. SIGMA: Revista de Matemática, 32, 103-130. Recuperado de http://www.hezkuntza.ejgv.euskadi.eus/r43-573/es/contenidos/informacion/dia6_sigma/es_sigma/adjuntos/sigma_32/8_pitagoras.pdf

Grupo Nación (2011). Libros para todos de GN: Matemáticas 9 año. San José, Costa Rica: Grupo Nación S.A.

Guardia, D.; Montes, F.; Páez, S. E. y Schmidt-Kortenbusch, T. (2009). Unidad didáctica del teorema de Pitágoras. Trabajo realizado en el marco de la asignatura de Didáctica de la Matemática de la Licenciatura de Matemáticas de la Universidad de Granada. (Documento no publicado). Universidad de Granada, España.

Jiménez, R. (2005). Geometría y trigonometría para noveno (primera edición). San José, Costa Rica: Academia de Matemática AMP.

Joyce, D. (1996). Euclid’s Elements. Worcester, Boston, United States of America: Clark University. Recuperado de https://mathcs.clarku.edu/~djoyce/elements/bookI/propI47.html

Marín, M. (2011). Teorema de Pitágoras (Tesis de Maestría). Universidad de Granada, España.

Martínez, A. (2000). Teorema de Pitágoras: originalidad de las demostraciones de E. García Quijano (1848). La Gaceta, 3(2), 277-296.

Meavilla, V. (1989). Dos demostraciones dinámicas del Teorema de Pitágoras. SUMA, 3, 39-42.

Ministerio de Educación Pública [MEP] (2012). Programas de estudio de Matemáticas. San José, Costa Rica. Recuperado de https://www.mep.go.cr/sites/default/files/programadeestudio/programas/matematica.pdf

Motta, H. y Opazo, E. (2012). Uma revisão do teorema de pitágoras e seu ensino. En J. E. Creste (Ed.), Anais do Encontro de Ensino, Pesquisa e Extensão (ENEPE) (p. 11). Brasil: Universidade do Oeste Paulista. Recuperado de http://www.unoeste.br/site/enepe/2012/anais/arquivos/pdfs/Exatas/Matematica.pdf

Osorio, L. (2011). Representaciones semióticas en el aprendizaje del teorema de Pitágoras (Tesis de Maestría). Universidad Autónoma de Manizales, Colombia.

Peñafiel, A. y Yun, J. (2008). El teorema de Pitágoras con frijoles de goma. Revista Educación Matemática, 1(20), 103-113.

Perry, P. (2000). Una propuesta para abordar el Teorema de Pitágoras en clase. Revista EMA, 2(5), 152-169. Recuperado de http://funes.uniandes.edu.co/1109/1/65_Perry2000Una_RevEMA.pdf

Pinto, J. (2012). Pitágoras e Van Hiele: uma possibilidade de conexão Pythagoras and Van Hiele: a possible connection. Ciência & Educação, 3(18), 643-655. doi: https://doi.org/10.1590/s1516-73132012000300010

Polya, G. (1989). Cómo plantear y resolver problemas. México DF, México: Editorial Trillas.

Real Academia Española [RAE] (2019). Diccionario de la lengua española. Madrid, España: Autor. Recuperado de https://dle.rae.es/?id=HlH0iLR

Rico, L. (1997). Los organizadores del currículo de matemáticas. En L. Rico (Ed.), La educación matemática en la enseñanza secundaria (pp. 39-59). Barcelona, España: Horsori.

Rico, L. (2003). El método del análisis didáctico. UNION, 33, 11-27. Recuperado de http://www.fisem.org/www/union/revistas/2013/33/ARCHIVO6.pdf

Rico, L. (2013). El método del análisis didáctico. Revista Iberoamericana de Educación, 33, 11-27.

Rico, L. y Fernández-Cano, A. (2013). Análisis didáctico y metodología de investigación. En L. Rico, J. Lupiáñez y M. Molina (Eds.), Análisis Didáctico en Educación Matemática (pp. 1-22). Granada, España: Comares.

Rico, L., Marín, A., Lupiáñez, J. y Gómez, P. (2008). Planificación de las matemáticas escolares en secundaria. El caso de los números naturales. SUMA, 58, 7-23.

Rico, L.; Lupiáñez, J.; Marín, A. y Gómez, P. (2007). Matemáticas escolares y análisis de contenido con profesores de secundaria en formación. Comunicación presentada en VIII Seminario de Investigación Pensamiento Numérico y Algebraico (PNA) de la SEIEM, Aravaca, España. Recuperado de http://funes.uniandes.edu.co/466/1/RicoL07-2848.PDF

Rico. L. y Moreno, A. (2016). Elementos de didáctica de la matemática para el profesor de secundaria. Granada, España: Pirámide.

Rojas, N. (2014). Caracterización del conocimiento especializado del profesor de matemáticas: un estudio de casos (Tesis de doctorado). Universidad de Granada, España. Recuperado de http://funes.uniandes.edu.co/6428/2/Rojas2013ConocimientoProfesor.pdf

Ruiz, C. (2000). ¿Cómo y qué se recuerda del teorema de Pitágoras? Ciencia y Desarrollo (Bib. Agronomía), 26(151), 66-73 Recuperado de https://www.researchgate.net/publication/32931614_Como_y_que_se_recuerda_del_teorema_de_pitagoras

Segovia, I. y Rico, L. (2001). Unidades didácticas. Organizadores. En E. Castro (Ed.), Didáctica de la matemática en la educación primaria (pp. 83-104). Madrid, España: Síntesis.

Strathern, P. (2014). Pitágoras y su teorema en 90 minutos. Madrid, España: Siglo XXI.

Sutton, K. (2012). A study of students’ misconceptions regarding variables in the Pythagorean Theorem and slope/intercept formula (Tesis de Maestría). State University of New York at Fredonia, EE. UU.

Vargas, G. y Gamboa, R. (2013a). La enseñanza del teorema de Pitágoras: una experiencia en el aula con el uso del Geogebra, según el modelo de Van Hiele. Uniciencia, 27(1), 95-118. Recuperado de http://www.revistas.una.ac.cr/index.php/uniciencia/article/view/4945/4739

Vargas, G. y Gamboa, R. (2013b). El modelo de Van Hiele y la enseñanza de la geometría. Uniciencia, 27(1), 74-94. Recuperado de http://www.revistas.una.ac.cr/index.php/uniciencia/article/view/4944

¿Qué modos de uso propone el profesorado de matemáticas en formación inicial para la enseñanza del teorema de Pitágoras en educación secundaria? en Revista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported licence.