Caracterización de tareas evaluadas en exámenes universitarios de cálculo: un enfoque didáctico e histórico

Analyzing tasks assessed in university Calculus exams: a didactic and historical perspective

Caracterização de tarefas avaliadas em provas universitárias de cálculo: uma abordagem didática e histórica

María G. Calderón-Torres1*, Juan F. Ruiz- Hidalgo2

Received: Sep/7/2023 • Accepted: Jan/23/2024 • Published: Jul/31/2024

Resumen [Objetivo] El objetivo de este estudio es caracterizar tareas matemáticas evaluadas en exámenes, centrándose en rasgos didácticos relacionados con el significado de los contenidos matemáticos que tratan y con aspectos cognitivos. Así como describir la evolución de estos rasgos a través del tiempo. [Metodología] En este estudio descriptivo longitudinal se llevó a cabo un análisis de contenido de 568 tareas matemáticas evaluadas en 51 exámenes, a lo largo de 17 periodos lectivos consecutivos entre 2014 y 2022. El análisis se realizó en el contexto de un curso de Cálculo Diferencial e Integral impartido en una universidad en Costa Rica. La información se organizó e interpretó utilizando un sistema de siete variables relacionadas con rasgos didácticos propios del análisis de tareas matemáticas escolares. [Resultados] Las tareas matemáticas evaluadas se distinguen por variedad de contenidos y predominio de representación verbal-simbólica, situación científica exclusivamente matemática y demanda cognitiva a nivel de procedimientos sin conexiones. El predominio de las situaciones científicas exclusivamente matemáticas fue constante a lo largo del tiempo. Mientras que, a partir de cierto periodo, la representación verbal-simbólica y los procedimientos sin conexiones tendieron a disminuir a favor de la representación múltiple y de los procedimientos con conexiones. [Conclusiones] Las tareas matemáticas evaluadas reflejan parcialmente rasgos relacionados con el significado de los contenidos matemáticos y con aspectos cognitivos esenciales para el aprendizaje del cálculo. La evolución a lo largo del tiempo muestra que se ha progresado en ciertos rasgos, aunque en otros todavía existe un amplio margen de mejora. Palabras clave: análisis de tareas; cálculo; evaluación del estudiante; matemáticas; universidad. Abstract [Objective] This study seeks to characterize mathematical tasks assessed in exams, with a focus on didactic features related to the meaning of the mathematical content they address, and their cognitive aspects. Additionally, it aims to describe the evolution of these features over time. [Methodology] In this longitudinal descriptive study, a content analysis of 568 mathematical tasks from 51 exams was conducted over 17 consecutive academic periods between 2014 and 2022. The analysis was conducted within the context of a Differential and Integral Calculus course taught at a university in Costa Rica. Information was organized and interpreted using a system of seven variables related to didactic features specific to the analysis of school-level mathematical tasks. [Results] The assessed mathematical tasks stand out for their variety of content and a predominance of verbal-symbolic representation, exclusively mathematical scientific situations, and cognitive demand at the level of procedures without connections. The predominance of exclusively mathematical scientific situations remained constant over time. However, from a certain point onwards, there was a tendency for verbal-symbolic representation and procedures without connections to decrease in favor of multiple representations and procedures with connections. [Conclusions] The assessed mathematical tasks partially reflect features related to the meaning of mathematical content and cognitive aspects essential for learning calculus. The evolution over time indicates progress in several features, although there is still ample room for improvement in others. Keywords: Task analysis; calculus; student assessment; mathematics; university. Resumo [Objetivo] O objetivo deste estudo é caracterizar as tarefas matemáticas avaliadas em provas, concentrando-se em características didáticas relacionadas ao significado do conteúdo matemático abordado e aos aspectos cognitivos. Assim como descrever a evolução dessas características ao longo do tempo. [Metodologia] Neste estudo descritivo longitudinal, foi realizada uma análise de conteúdo de 568 tarefas matemáticas avaliadas em 51 provas durante 17 períodos letivos consecutivos entre 2014 e 2022. A análise foi realizada no contexto de um curso de Cálculo Diferencial e Integral ministrado em uma universidade da Costa Rica. As informações foram organizadas e interpretadas por meio de um sistema de sete variáveis relacionadas a características didáticas típicas da análise de tarefas matemáticas escolares. [Resultados] As tarefas matemáticas avaliadas se distinguem pela variedade de conteúdo e predominância de representação verbal-simbólica, situação científica exclusivamente matemática e demanda cognitiva no nível de procedimentos sem conexões. A predominância de situações científicas exclusivamente matemáticas foi constante ao longo do tempo. Ao passo que, depois de um certo período, a representação verbal-simbólica e os procedimentos sem conexões tenderam a diminuir em favor da representação múltipla e dos procedimentos com conexões. [Conclusões] As tarefas matemáticas avaliadas refletem parcialmente características relacionadas ao significado do conteúdo matemático e aos aspectos cognitivos essenciais para o aprendizado de cálculo. A evolução ao longo do tempo mostra que houve progresso em determinadas características, embora em outras ainda haja muito espaço para melhorias. Palavras-chave: análise de tarefas; cálculo; avaliação de alunos; matemática; universidade.

Introducción

En enseñanza matemática, la evaluación del aprendizaje estudiantil mediante exámenes escritos es una práctica común que se prevé continuará siendo relevante en el futuro, tanto en evaluaciones a gran escala como en el ámbito de las aulas (Suurtamm et al., 2016). Este tipo de pruebas, junto con las tareas matemáticas que los componen, desempeñan un rol fundamental. A menudo, tanto docentes como estudiantes los consideran modelos de lo que se debe enseñar y aprender, incluso por encima de lo expresado en los planes de estudio (Swan y Burkhardt, 2012).

Por lo tanto, el análisis de estas evaluaciones permite comprender, de manera indirecta, el enfoque de las actividades de enseñanza y el alcance de los resultados del aprendizaje, y compararlos con los objetivos de aprendizaje de la educación matemática declarados a nivel curricular. Si las evaluaciones no reflejan lo esencial que el estudiantado debe aprender sobre matemáticas, entonces las actividades de enseñanza y los resultados del aprendizaje reflejarán ese desequilibrio (Suurtamm et al., 2016; Swan y Burkhardt, 2012).

Los enfoques curriculares en diferentes partes del mundo presentan notables similitudes en cuanto a las metas de aprendizaje consideradas esenciales en la educación matemática (Askew et al., 2010). A pesar de su elevada importancia en el plan de estudios, estas metas a menudo no se manifiestan en las evaluaciones, que suelen enfocarse de manera aislada en contenidos específicos y habilidades técnicas (Swan y Burkhardt, 2012).

Estos enfoques curriculares comparten una visión integral que coloca la resolución de problemas en diversos contextos en un lugar central y las metas de aprendizaje buscan un equilibrio entre habilidades, procesos, conceptos y procedimientos. Por un lado, las habilidades y procesos se expresan comúnmente mediante prácticas matemáticas fundamentales, tales como razonar, argumentar, establecer conexiones, representar, dar sentido, comunicar, modelar, entre otras. Por otro lado, los conceptos y procedimientos se concretan en términos de contenidos o saberes, que abarcan áreas como números, álgebra, medidas, geometría, entre otras. Ejemplos de esta perspectiva se pueden observar en los estándares curriculares estadounidenses (National Council of Teachers of Mathematics [NCTM], 2000; National Governors Association Center for Best Practices and Council of Chief State School Officers [NGA y CCSSO], 2010) y en los planes de estudio de matemáticas de países como Singapur (Soh, 2008), España (Ministerio de Educación y Formación Profesional, 2022) y Costa Rica (Ministerio de Educación Pública [MEP], 2012).

Parece evidente que las evaluaciones deberían reflejar lo que es esencial aprender sobre matemáticas, no solo en términos de contenidos sino también de prácticas y habilidades matemáticas fundamentales (NCTM, 1995; Swan y Burkhardt, 2012). En particular, interesa determinar si los exámenes, en términos del diseño de las tareas matemáticas que los componen, evalúan la naturaleza compleja del pensamiento matemático, la resolución de problemas y otras competencias sustanciales definidas en los currículos (Suurtamm et al., 2016).

Dada su relevancia, se han realizado múltiples estudios sobre análisis de tareas de evaluación en matemáticas, en diversos contextos y niveles educativos. Por ejemplo, Caraballo et al. (2011) examinaron características de tareas de evaluación diagnóstica para estudiantes de secundaria en España. Sus hallazgos revelaron equilibrio en cuanto a contenido y predominio del contexto público y del nivel de complejidad de reproducción, así como escasez de competencias relacionadas con la modelización, la argumentación, el razonamiento y la resolución de problemas.

En otro estudio, Ruiz-Hidalgo et al. (2019) se enfocaron en describir tareas de cálculo en pruebas de acceso a la universidad de distintas comunidades autónomas españolas. Concluyeron que las tareas más comunes eran enunciadas de forma verbal-simbólica, con la meta de aplicar procedimientos en situaciones meramente matemáticas. También, Bhaird et al. (2017) analizaron las oportunidades para el razonamiento creativo en exámenes y tareas evaluadas en cursos de cálculo de primer año de universidades irlandesas. Sus resultados indicaron que en las tareas examinadas predomina el razonamiento algorítmico.

Por su parte, Gaona y Vivier (2022) llevaron a cabo un estudio para caracterizar el valor epistémico de tareas en un sistema de evaluación en línea para matemáticas en una universidad chilena. Observaron que las tareas tendían a privilegiar el uso de contextos artificiales y el trabajo instrumental, haciendo un uso rutinario de fórmulas, así como el trabajo semiótico mediante la lectura de gráficos y la conversión de registros (algebraico, gráfico, natural). Asimismo, García-Oliveros et al. (2020) examinaron el contexto, el contenido y la exigencia cognitiva de tareas matemáticas empleadas para realizar evaluaciones en cursos universitarios introductorios en Colombia. Sus hallazgos mostraron que los conocimientos procedimentales predominan en las tareas analizadas.

El interés en el análisis de las tareas matemáticas se ha reflejado no solo en investigaciones centradas en las evaluaciones que las contienen, sino también en estudios relacionados con libros de texto que las incorporan, e incluso en investigaciones que abarcan esos dos ámbitos (White y Mesa, 2014). Así como en el caso de las evaluaciones, varios de estos estudios han identificado indicios de falta de coherencia entre los estándares para la educación matemática y ciertos rasgos de las tareas, como su nivel de demanda cognitiva (Ramos y Casas, 2018) o el significado de los contenidos matemáticos que promueven (Balcaza et al., 2017; Vargas et al., 2020).

Este estudio se enfoca en analizar tareas matemáticas evaluadas en exámenes universitarios de Cálculo Diferencial e Integral, siguiendo la línea de investigaciones sobre tareas matemáticas de evaluación. Además de llevar a cabo un análisis didáctico de características específicas de estas tareas, se realiza un análisis histórico para conocer cómo han evolucionado con el tiempo. En otras palabras, el objetivo principal de este estudio es caracterizar las tareas matemáticas utilizadas para evaluar, identificando los rasgos que han permanecido constantes y aquellos que han cambiado a lo largo de los años.

Si bien el enfoque principal es comprender las características de las tareas evaluadas en los exámenes y su evolución, con el propósito de contextualizar y enriquecer esta comprensión, también se describen los sistemas de evaluación a los que pertenecen los exámenes y sus tareas.

En este estudio se examinó la evaluación implementada entre 2014 y 2022 (ambos años inclusive) en un curso convencional de cálculo (White y Mesa, 2014) impartido en una universidad de Costa Rica. De manera similar a lo que ocurre en otros cursos de Cálculo de otras universidades del mundo, este curso está diseñado para introducir a grupos numerosos de estudiantes de diversas disciplinas (ingenierías, química, biología, economía, entre otras) en los conceptos y herramientas básicas del cálculo diferencial e integral en una variable (límites y continuidad, derivada y sus aplicaciones e integrales y sus aplicaciones) como herramientas prácticas en el desarrollo de sus carreras.

Este estudio ofrece un punto de referencia para el profesorado de cursos convencionales de cálculo en diversas universidades, incentivándolos a reflexionar sobre sus propias prácticas de evaluación. Dado que las metas de aprendizaje actuales en educación matemática hacen hincapié en el desarrollo de conocimientos tanto de contenido como de procesos que reflejen la complejidad del pensamiento matemático, resulta fundamental que el profesorado considere adaptar sus prácticas de evaluación (Suurtamm et al., 2016). El diseño de las evaluaciones, en particular la diversidad y el equilibrio de las tareas matemáticas en los exámenes, tiene un potencial significativo para impulsar mejoras, pues, en la práctica, a menudo representan el nivel máximo de aprendizaje que se logra en la mayoría de las aulas (Swan y Burkhardt, 2012). Además, este estudio ilustra cómo el contexto y la teoría influyen en las prácticas de evaluación (De la Orden y Pimienta, 2016).

Marco conceptual de referencia

Según Rico (2013), el currículo se define como todo programa de formación, definido por su tipo y finalidades, incluyendo normas, valores, conocimientos, habilidades, entre otros aspectos. Este concepto también abarca a los sujetos que se forman, los recursos institucionales, el personal docente y el sistema de evaluación. Rico (1997a) sostiene que el currículo y el trabajo curricular ―entendido como cualquier actividad de reflexión, planificación e implementación de un programa de formación― se pueden estructurar sistemáticamente en dimensiones y niveles. Esto implica especificar principios ideológicos, pedagógicos y psicopedagógicos, organizados en dimensiones para canalizar diferentes niveles de concreción, que van desde el sistema educativo general hasta las prácticas en un aula (Rico y Ruiz-Hidalgo, 2018).

Adicionalmente, en línea con las dimensiones curriculares y al considerar la especificidad del contenido matemático escolar, Rico (1997b) plantea la noción de organizador curricular, como un conjunto de categorías de análisis. Estos organizadores actúan como marcos conceptuales para la gestión del currículo en matemáticas, estructurando el conocimiento didáctico generado (Rico, 1997b) y permitiendo el análisis de textos de matemáticas escolares, en particular (Segovia y Rico, 2001).

Específicamente en el ámbito de la investigación, las dimensiones curriculares y sus organizadores no solo permiten focalizar los estudios, sino que también facilitan un método de investigación organizado, consistente y validado (Rico y Ruiz-Hidalgo, 2018).

Dentro de esta perspectiva curricular, el análisis didáctico se propone como un marco conceptual y metodológico de referencia propio de la educación matemática (Rico et al., 2013). Este estudio se apoya en dicho referente conceptual y metodológico para proporcionar una estructura organizativa e interpretativa a la investigación. Además, el enfoque se alinea con sus formas de aplicación en el campo.

El análisis didáctico se compone de cuatro tipos de análisis: de significados, cognitivo, de instrucción y evaluativo, que se identifican con las dimensiones cultural, cognitiva, normativa y social del currículo (Rico, 2016). En particular, el análisis de tareas matemáticas escolares es una de las partes clave del análisis de instrucción.

Moreno y Ramírez (2016) definen tarea matemática escolar como “una propuesta que solicita la actividad del alumno en relación con las matemáticas y que el profesor planifica” (p. 244) con intención de aprendizaje o de evaluación. Estos autores destacan variables que pueden utilizarse para describir una tarea, entre ellas: contenido, formulación-representación (simbólico, gráfico, numérico, verbal y pictórico), situación-contexto-dominio (extra o intramatemático), autenticidad, dificultad-complejidad (reproducción, conexión, y reflexión), meta-finalidad, estructura-formato (abierta y cerrada), dimensión (ejercicio y problema), tipo de agrupamiento, recursos-materiales y temporalización.

Al respecto, otros autores como Swan y Burkhardt (2012) señalan variables similares: lenguaje-estilo, contexto-autenticidad (tareas matemáticas puras, tareas auténticas, aplicaciones ilustrativas), dificultad (complejidad, duración, grado de desconocimiento, apertura), propósito, andamiaje-transparencia, eficiencia, accesibilidad y diferenciación.

Algunas de las variables identificadas por Moreno y Ramírez (2016) se relacionan con aspectos semánticos (del significado) o cognitivos (del aprendizaje). Por lo que el análisis de las tareas matemáticas escolares está estrechamente relacionado con los análisis de significados y cognitivo, dos dimensiones clave del análisis didáctico.

Para el estudio de los significados de un contenido matemático escolar se consideran tres organizadores o componentes: estructura conceptual, sistemas de representación y sentidos y modos de uso. La estructura conceptual está constituida por una red de hechos, conceptos, relaciones, procedimientos, destrezas, razonamientos y estrategias (Fernández-Plaza, 2016; Rico, 2016). Por su parte, los sistemas de representación (simbólico, gráfico, numérico, verbal y pictórico) organizan las representaciones mediante las que se expresan los conceptos y procedimientos matemáticos (Castro y Castro, 1997; Lupiáñez, 2016). Mientras que, los sentidos y modos de uso de un contenido matemático se denotan a través de los fenómenos en donde surgió, las situaciones en las que interviene y los contextos a los que pertenecen las cuestiones a las que responde (Ruiz-Hidalgo, 2016).

En el caso del análisis cognitivo de las condiciones y orientaciones del aprendizaje matemático escolar se consideran, entre otros, elementos como: las expectativas y las oportunidades de aprendizaje. Las primeras se expresan en forma de objetivos o competencias y hacen referencia a capacidades (acciones observables), conocimientos específicos y contextos (Flores y Lupiáñez, 2016). Mientras que las demandas cognitivas, sus facetas (formular, aplicar e interpretar) y sus niveles de complejidad (reproducción, conexión y reflexión) forman parte de las oportunidades de aprendizaje (Ruiz-Hidalgo y Rico, 2016).

El análisis evaluativo, último tipo dentro del marco del análisis didáctico, cobra relevancia cuando se emplean tareas matemáticas escolares para medir el progreso o el logro de los estudiantes en cuanto a su aprendizaje. Este análisis se enfoca, entre otros aspectos, en el diseño de las evaluaciones y en sus indicadores de calidad (Segovia, 2016). En particular, sobre el diseño de tareas matemáticas de evaluación y sus estándares de calidad, diversos autores (NCTM, 1995; Swan y Burkhardt, 2012; Van den Heuvel-Panhuizen y Becker, 2003; Watson y Ohtani, 2015) coinciden al señalar que estas tareas deben reflejar: (a) diversidad y equilibrio en los procesos o prácticas matemáticas, tales como argumentar, representar y resolver problemas, incluso por encima de la diversidad de contenidos o dominios temáticos; (b) variedad de situaciones y contextos matemáticos y extramatemáticos, evitando situaciones artificiales; (c) amplitud de niveles de demanda cognitiva y (c) multiplicidad de dependencias, relaciones, soluciones y vías de solución.

Metodología

Con el objetivo de caracterizar las tareas matemáticas empleadas para evaluar e identificar rasgos que se mantienen consistentes o cambian a lo largo del tiempo, en este estudio descriptivo longitudinal (Cohen et al., 2017) se siguió el método de análisis de contenido (Krippendorff, 2019; Rico y Fernández-Cano, 2013). En total, se examinaron 51 exámenes y 568 tareas matemáticas.

Recolección de datos

Se consideró el contenido de todas las tareas matemáticas que formaron parte del total de exámenes escritos evaluados en un curso de cálculo impartido en una universidad de Costa Rica, seleccionada para este estudio debido a la disponibilidad de acceso a los datos.

Se contemplaron los 17 periodos lectivos consecutivos en los que la asignatura se impartió en su formato actual, desde el año 2014 y hasta el 2022 (cierre de la recogida de datos). En ese lapso, el curso se desarrolló dos veces al año, excepto en 2014 cuando únicamente se impartió en el segundo periodo lectivo. No cabe duda de que la pandemia por Covid-19 representa un intervalo de tiempo que se considera diferenciado por sus características singulares. Sin embargo, se mantuvo el criterio cronológico para observar qué información proporcionan los datos.

Análisis de datos

Los exámenes están formados por ejercicios, algunos de los cuales poseen varios apartados. A pesar de que los apartados de un mismo ejercicio pueden estar relacionados de alguna manera, se pueden analizar de forma independiente. En consideración de lo anterior, la unidad de análisis de este estudio, denominada tarea, fue cada apartado de un ejercicio (en el caso de ejercicios con apartados) o simplemente cada ejercicio (cuando no tenía apartados).

Para analizar cada tarea, la información contenida en su enunciado se interpretó a través de un sistema de variables. Este proceso implicó el registro y la organización de los datos en una matriz, la cual asoció cada tarea con una categoría específica dentro de las consideradas para cada variable. Utilizando las funciones avanzadas de hojas de cálculo, como tablas y gráficos dinámicos, el software Excel facilitó tanto el registro como el análisis exhaustivo del voluminoso conjunto de datos generados por el estudio.

A continuación, se describe el sistema de siete variables empleado:

1. Contenido: concreta, de la manera más precisa y específica posible, el contenido matemático referido en la tarea, dentro del ámbito del Cálculo Infinitesimal (Ruiz-Hidalgo et al., 2019). Adicionalmente, se registró el tema general, denominado unidad de contenido, el cual corresponde al contenido específico de cada tarea. Se registraron cinco unidades de contenido: límites y continuidad, derivación, aplicaciones de la derivada, integración y aplicaciones de la integral. Por ejemplo, los contenidos específicos de la unidad de contenido derivación son: derivación por teoremas, derivación de orden superior, derivación implícita, derivación logarítmica, derivada por definición, rectas tangente y normal, derivada en un punto y teorema de Rolle.

2. Representación: describe el sistema de representación en que se expresa o formula la tarea (Ruiz-Hidalgo et al., 2019; Vargas et al., 2020). Puede ser: solo verbal, verbal-simbólico, verbal-gráfico, verbal-geométrico o múltiple.

3. Situación: se refiere al contexto en que se propone la tarea. Se consideraron las situaciones enlistadas en el marco PISA (Organization for Economic Co-operation and Development [OECD], 2016): personal, educativa-laboral, público-social y científica. Sin embargo, así como (Ruiz-Hidalgo et al., 2019) se hizo una distinción entre situaciones científicas exclusivamente matemáticas o científico-tecnológicas no exclusivamente matemáticas.

4. Demanda: indica el nivel de demanda cognitiva prevista, según las características de los procesos implicados en realizar la tarea (Smith y Stein, 1998). Se definen cuatro niveles de demanda cognitiva: memorización (no se usan algoritmos, se recurre, sin necesidad de explicaciones, a datos recordados o tomados directamente del enunciado), procedimiento sin conexiones (uso de algoritmos, pero sin necesidad de establecer conexiones con aspectos distintos al procedimiento mismo, o de dar explicaciones más allá de lo que al procedimiento se refiere), procedimientos con conexiones (uso de algoritmos, pero con la necesidad de establecer y explicar conexiones con aspectos distintos al procedimiento, de manera que conocer un algoritmo no es suficiente para resolver) y hacer matemática (estrategia de solución no predeterminada, incluyendo necesidad de establecer y explicar conexiones entre aspectos de la estrategia como conceptos, procesos y propiedades).

5. Acción: concreta, por medio de un verbo en infinitivo, la acción explícita requerida según el enunciado de la tarea. Puede ser: calcular, determinar, explicar, resolver, trazar, usar, verificar, estudiar, identificar o justificar. Esta variable y sus categorías emergieron del análisis.

6. Dirección: identifica el rumbo previsto en que se deben realizar las acciones para determinar lo solicitado en la tarea (Martinez-Luaces et al., 2018). Puede ser: rumbo directo (dados elementos iniciales, se aplican procedimientos sobre ellos para determinar aspectos que los caracterizan) o rumbo inverso (dadas condiciones iniciales, se aplican procedimientos para determinar los elementos que las satisfacen).

7. Relación: describe el tipo de relación de una tarea con otras del mismo examen escrito en que se presenta (Ruiz-Hidalgo et al., 2019). Producto del análisis de los datos, se identificó: relación nula, relación solamente de enunciado (la tarea no comparte información sobre la función matemática implicada, los datos o la solución de otra tarea), relación solamente de información (la tarea comparte con otra información sobre la función matemática o los datos implicados, pero sus soluciones no presentan dependencia), relación de información y solución (la tarea comparte con otra información y sus soluciones presentan dependencia).

Este sistema de variables se determinó de manera similar a lo realizado en otros estudios sobre análisis de tareas matemáticas (Martinez-Luaces et al., 2018; Ruiz-Hidalgo et al., 2019; Vargas et al., 2020). Primero se tomaron en cuenta aspectos señalados como relevantes en el caso de las tareas matemáticas escolares, definidos por Moreno y Ramírez (2016) dentro del marco de referencia del análisis didáctico (Rico et al., 2013; Rico y Moreno, 2016). Luego, algunos de estos aspectos se adaptaron en función de las observaciones sugeridas durante el proceso de análisis, así como siguiendo las recomendaciones de otros autores. Por ejemplo, la variable denominada demanda cognitiva, descrita en el análisis didáctico mediante los tres niveles de complejidad (reproducción, conexión y reflexión) de PISA (OECD, 2016), en este estudio se concretó según los cuatro niveles del modelo de la demanda cognitiva de Smith y Stein (1998): memorización, algoritmos sin conexiones, algoritmos con conexiones y hacer matemática.

Este modelo de cuatro niveles (Stein et al., 1996) fue utilizado por Vargas et al. (2020). Previamente, Ruiz-Hidalgo et al. (2019) señalaron la dificultad que supone clasificar ciertas tareas matemáticas utilizando los tres niveles de complejidad del marco PISA, al considerarlos insuficientes para describir algunas diferencias que influyen en la complejidad de las tareas.

De forma similar a lo realizado por Ruiz-Hidalgo et al. (2019) y Vargas et al. (2020), para organizar e interpretar los datos, las variables se agruparon considerando los aspectos generales referidos en ellas: variables sobre el contenido y su significado (contenido, representación y situación) y variables sobre aspectos cognitivos (demanda, acción, dirección y relación).

La Figura 1 ilustra y detalla el proceso utilizado para recoger y analizar las tareas matemáticas evaluadas en los exámenes. Además, destaca cómo el análisis didáctico cumple una función organizadora e interpretativa en este estudio. Mediante las dimensiones curriculares y sus organizadores, la investigación se sitúa dentro del marco del análisis evaluativo. La necesidad de examinar las tareas matemáticas escolares conlleva el empleo de los organizadores específicos del análisis de instrucción. Estos, a su vez, se basan en el estudio de los significados presentes en los contenidos matemáticos y en el análisis cognitivo.

Figura 1. Resumen y ejemplo del proceso de análisis de las tareas evaluadas en los exámenes

Nota: elaboración propia.

Análisis complementario

Si bien el enfoque principal de este estudio son las características de las tareas matemáticas evaluadas en los exámenes y su evolución a través del tiempo, con el fin de contextualizar y enriquecer la comprensión general de los resultados, también se examinó los sistemas de evaluación a los que pertenecen los exámenes y sus tareas. Se realizó un análisis de contenido del programa de estudio correspondiente a cada uno de los 17 periodos lectivos en que se evaluaron los exámenes analizados.

Se destaca que, en cada periodo, el programa de estudio fue uniforme para todos los grupos en los que se dividió la población de estudiantes del curso, junto con el personal docente asignado. Esta uniformidad en el programa se basa en una norma institucional conocida como “trabajo en cátedra”.

El programa de estudio abarca diversos aspectos, los cuales incluyen elementos generales como modalidad, créditos y requisitos; además de contenidos, objetivos, estrategias metodológicas, criterios de evaluación, entre otros componentes.

Para describir los sistemas de evaluación implementados en el curso se utilizó un conjunto de variables. Estas corresponden a cinco dimensiones de la evaluación (objeto, método, sujeto, momento y propósito), que en la literatura científica se utilizan para caracterizar diferentes enfoques o sistemas evaluativos en educación: a gran escala y en el aula (Suurtamm et al., 2016), profunda y superficial (Sánchez, 2011), o para el aprendizaje, formativa y sumativa (Black y William, 1998; De la Orden y Pimienta, 2016; Sadler, 1989; Stiggings, 2014).

Respectivamente, las dimensiones de la evaluación citadas responden a las preguntas: ¿qué se evalúa?, ¿cómo se evalúa?, ¿quién evalúa a quién?, ¿cuándo se evalúa? y ¿para qué se evalúa? Por ejemplo, el objeto de la evaluación puede ser un objetivo o una competencia definida en un programa de estudios para delimitar los aprendizajes esperados. Un examen escrito u oral, un portafolio, un proyecto u otro puede ser el método de evaluación, y esto podría hacerse en línea o con apoyo de recursos tecnológicos, o prescindiendo de ello. Puede ser el o la docente quién evalúa al estudiante, o bien, el estudiante puede evaluar a sus pares o a sí mismo. Incluso, se puede evaluar antes de iniciar un proceso educativo, continuamente, por etapas o al cabo del proceso. Y, puede evaluarse con el propósito de certificar un logro, dar una calificación, determinar la promoción, determinar intervenciones, mejorar los procesos de enseñanza-aprendizaje, identificar dificultades u obstáculos, retroalimentar, autorregular el aprendizaje o diagnosticar.

Análisis y resultados

El enfoque principal de este estudio es la comprensión de las características de las tareas evaluadas en los exámenes y su evolución. No obstante, para contextualizar y enriquecer la comprensión de los resultados, se describen los sistemas de evaluación en los que estos exámenes y sus tareas se integran.

Sistemas de evaluación de los exámenes y sus tareas

De acuerdo con el contenido de los 17 programas de estudio analizados, algunas características de los sistemas de evaluación se mantuvieron constantes a lo largo del tiempo, mientras que otras variaron en mayor o menor medida.

Respecto al objeto de la evaluación, en los programas se manifiesta que los aspectos a evaluar son los contenidos (59 %), el trabajo de la persona (35 %) o no se especifica (6 % restante). En todos los casos, los contenidos se presentaron agrupados en áreas temáticas (límites de funciones reales de variable real, derivadas, aplicaciones de la derivada, integrales y aplicaciones de la integral), cuyos elementos específicos prácticamente no variaron a través del tiempo.

Aunque en todos los programas se establecen objetivos para delimitar los aprendizajes esperados, en ningún caso se hace referencia a estos objetivos como puntos de la evaluación. El objetivo general declarado siempre fue resolver problemas de aplicación utilizando conceptos del cálculo diferencial e integral. Mientras que los objetivos específicos variaron a partir del primer periodo del 2018 (comprender conceptos de límite de una función en una variable, derivada, integral indefinida, integral definida, calcular límites e integrales mediante diferentes métodos, resolver problemas que requieren calcular derivadas y optimizar funciones), pues previamente incluían menor detalle (desarrollar conceptos, resolver problemas mediante cálculo de derivadas e integrales y optimizar funciones).

Evaluar con exámenes escritos fue un método de la evaluación en todos los casos. Sin embargo, entre periodos se presentaron ciertas variaciones respecto al tipo de examen (parciales o cortos), medio de aplicación (papel y lápiz o en línea) y presencia de técnicas complementarias (portafolio, exposición y otras actividades).

Desde el 2014 y hasta el segundo periodo del 2019, se evaluó con exámenes escritos parciales a papel y lápiz. Durante ese lapso, en algunos momentos también se realizaron exámenes cortos, a papel y lápiz en el 2015 y en línea a partir del segundo periodo del 2018. En el 2020 y 2021, debido a la pandemia por Covid-19, todas las evaluaciones se aplicaron en línea con apoyo de recursos tecnológicos. Durante ese tiempo, en todos los casos se evaluó mediante exámenes escritos parciales en línea acompañados de otros métodos: exámenes cortos en línea (primer periodo del 2020), portafolio y exposición (segundo periodo del 2020 y primer periodo del 2021), así como otras actividades propuestas por cada docente de manera individualizada para su grupo de estudiantes, pero no descritas en el programa (segundo periodo del 2021). Finalmente, en el 2022 se evaluó nuevamente con exámenes parciales escritos a papel y lápiz, combinado con actividades individualizadas propuestas por cada docente.

Ahora bien, con respecto al sujeto de la evaluación, se observó que en todos los casos fue la persona docente quién diseñó y calificó las evaluaciones del alumnado. En ninguno de los programas se localizó alguna referencia a la evaluación entre estudiantes o a sí mismos y mismas. Respecto al docente como sujeto evaluador, se observó que todos los exámenes escritos (a papel y lápiz, en línea, parciales y cortos) fueron diseñados por el equipo docente para ser aplicados a todos los grupos por igual. Mientras que, otros métodos (portafolio, exposición y actividades individualizadas) fueron diseñados por cada docente en particular para sus estudiantes.

En todos los casos, el momento de la evaluación se llevó a cabo por etapas; pues, en los programas se mencionaron evaluaciones parciales aplicadas en diferentes momentos a lo largo del desarrollo del curso. En ningún caso se aludió a una evaluación antes de iniciar o al cabo del curso.

Dar una calificación y determinar la promoción fue un propósito de la evaluación claramente referido a lo largo del tiempo. En cada programa se detalló una explicación sobre la nota mínima para aprobar el curso y la forma en que se calcularía a través de valores porcentuales otorgados a las diferentes evaluaciones. No se localizaron referencias directamente atribuibles a otros propósitos como: determinar intervenciones, mejorar los procesos de enseñanza-aprendizaje, identificar dificultades u obstáculos, retroalimentar, autorregular el aprendizaje o diagnosticar.

Con respecto a la calificación, se identificó que el valor porcentual de los exámenes parciales siempre fue considerablemente mayor en comparación con otros métodos (exámenes cortos, portafolio, exposición y otras actividades). Este porcentaje osciló entre 100 % y 80 %, excepto en el segundo ciclo del 2021, cuando constituyó el 60 % de la nota final del curso.

En resumen, el personal docente fue el único responsable de diseñar y calificar las evaluaciones, sin participación del estudiantado en la evaluación de sus pares o de sí mismos(as). Predominó la evaluación de los contenidos y del trabajo de cada estudiante en exámenes parciales, realizados por etapas a lo largo del curso, a los cuales se les asignó un peso significativo en la calificación final. De esta manera, la calificación y la promoción fueron los únicos aspectos de la evaluación explícitamente declarados.

Sin embargo, hubo algunas variaciones a través del tiempo: inclusión de métodos complementarios (exposición, portafolio, otras actividades) y uso de diferentes medios de aplicación (papel y lápiz, en línea), principalmente. Varios cambios coincidieron con la etapa de adaptaciones ante la pandemia por Covid-19, posteriormente manteniéndose algunos (otras actividades además de exámenes escritos) y eliminándose otros (exámenes en línea).

Tareas matemáticas evaluadas en los exámenes

Se analizó el contenido de 568 tareas matemáticas evaluadas en 51 exámenes escritos parciales, los cuales corresponden a los 17 periodos en que el curso se impartió desde el 2014 hasta el 2022. Debido a la disparidad en las cantidades de tareas evaluadas entre periodos (Gráfica 1), el análisis de las características de cada una se realizó en términos porcentuales.

Gráfica 1. Cantidad de tareas matemáticas evaluadas en los exámenes analizados, según periodo

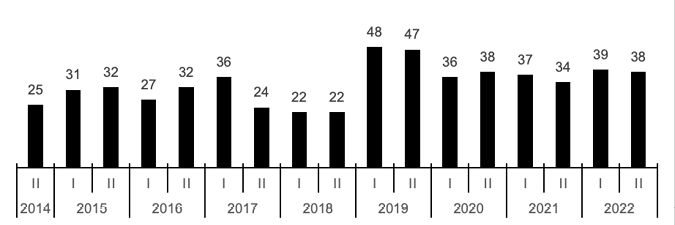
Nota: fuente propia de la investigación.

Para organizar e interpretar los resultados del análisis de las características de las tareas matemáticas evaluadas, se consideraron dos tipos de rasgos: características sobre los significados del contenido matemático (contenido, representación y situación) y características sobre aspectos cognitivos (demanda, acción, dirección y relación).

Significados del contenido matemático en las tareas evaluadas

En relación con el contenido matemático y sus significados, se estudió el contenido (unidad de contenido y contenido específico), la representación y la situación referenciada en cada tarea.

Respecto a la unidad de contenido en las que se agrupan los contenidos específicos del cálculo, aplicaciones de la derivada predomina (37 % del total de tareas), seguida por límites y continuidad (24 %), derivación e integración (17 % cada una) y aplicaciones de la integral (5 % restante). El valor relativo dado a cada unidad de contenido no varió considerablemente a lo largo del tiempo (Gráfica 2). A excepción de ciertos periodos (segundo periodo del 2016, primer periodo del 2017 y primer periodo del 2020) en los que las aplicaciones de la derivada disminuyeron su frecuencia a favor de límites y continuidad.

Gráfica 2. Distribución porcentual de tareas por periodo, según unidad de contenido

Nota: fuente propia de la investigación.

En particular, en lo que concierne a los contenidos específicos se contabilizan 36 en total; en promedio 7 por unidad de contenido. Los límites y la continuidad presentan mayor diversidad (10 contenidos específicos), mientras que las aplicaciones de la integral es la unidad de contenido menos diversa (2 contenidos específicos).

En el caso de la unidad de contenido de las aplicaciones de la derivada, los contenidos específicos más frecuentes fueron: regla de L´Hopital e interpretación gráfica de la primera derivada. No obstante, regla de L´Hopital estuvo presente a través del tiempo, mientras que, la interpretación gráfica de la primera derivada, solamente a partir del segundo periodo del 2019 (Gráfica 3). Además, la interpretación gráfica de la segunda derivada solo se presentó en el primer periodo del 2021.

Gráfica 3. Distribución porcentual de tareas sobre aplicaciones de la derivada, por periodo y contenidos específicos

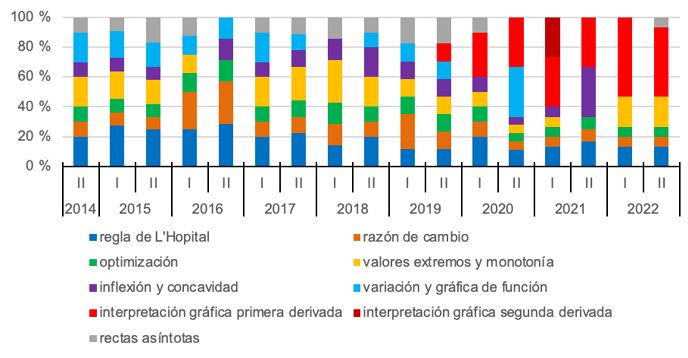
Nota: fuente propia de la investigación.

En el caso de la unidad de contenido límites y continuidad, el límite unilateral es el contenido específico más frecuente (35 % del total), pero no estuvo presente a lo largo del tiempo (Gráfica 4), a diferencia del límite al infinito (26 %) y continuidad (15 %), que sí se presentaron en todos los periodos. Además, el límite por teorema del encaje solo se encontró en el primer periodo del 2015 y en el segundo periodo del 2020.

Gráfica 4. Distribución porcentual de tareas sobre límites y continuidad, por periodo y contenidos específicos

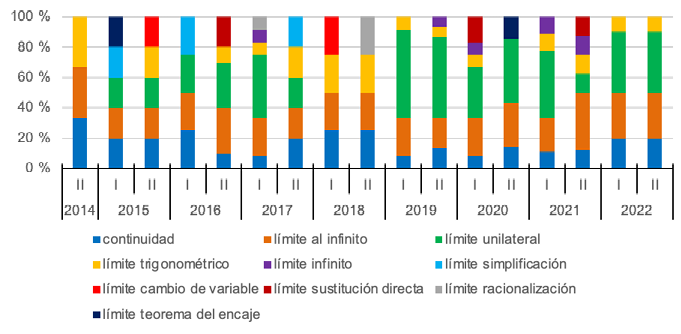
Nota: fuente propia de la investigación.

En el caso de la unidad de contenido “derivación”, los contenidos específicos más frecuentes son: derivación por teoremas (26 % del total), rectas tangente y normal (17 %), derivada de orden superior (16 %) y derivación implícita (15 %). Sin embargo, ninguno estuvo presente en todos los periodos (Gráfica 5). Además, el teorema de Rolle solo se presentó en el primer periodo del 2019.

Gráfica 5. Distribución porcentual de tareas sobre derivación, por periodo y contenidos específicos

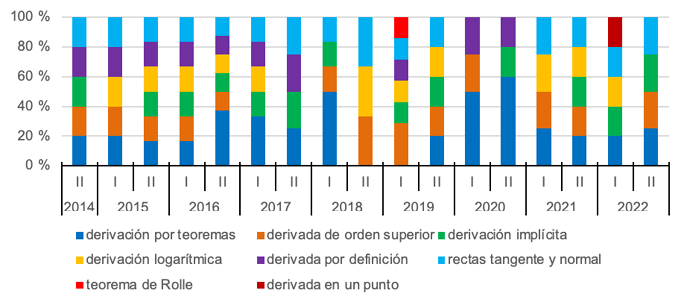
Nota: fuente propia de la investigación.

En el caso de las unidades de contenido “integración y aplicaciones de la integral”, los contenidos específicos más frecuentes son: áreas (22 % del total), integral indefinida por sustitución y sustitución trigonométrica (15 % cada una), por fracciones parciales (14 %) y por partes (13 %). De los cuales, solo la integral indefinida por sustitución trigonométrica y áreas se presentaron en todos los periodos (Gráfica 6). Además, sólidos de revolución únicamente se presentó antes de 2016. Sin embargo, cuando no se mostró tampoco estuvo en el programa de curso respectivo.

Gráfica 6. Distribución porcentual de tareas sobre integración y sus aplicaciones, por periodo y contenidos específicos

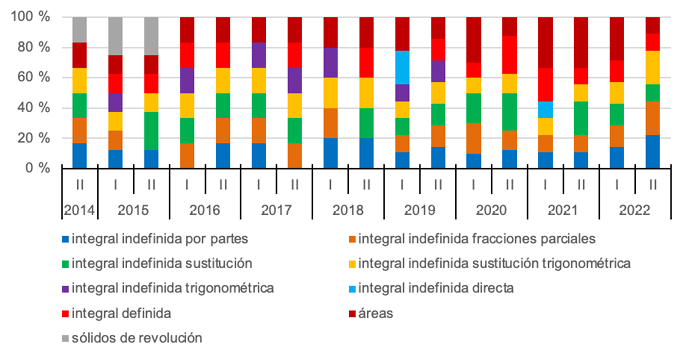
Nota: debido a que la unidad de contenido aplicaciones de la integral solamente presentó dos contenidos específicos, se presentan junto con los contenidos específicos de la unidad de contenido integración. Fuente propia de la investigación.

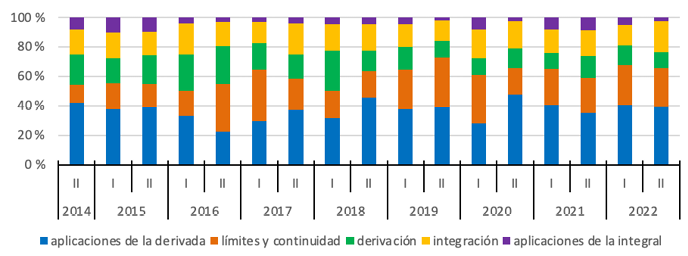
Respecto al sistema de representación en que se expresan las tareas, predomina el sistema verbal-simbólico, utilizado en 71 % del total de las tareas analizadas. En segundo lugar, el sistema múltiple (verbal, simbólico y gráfico o geométrico) fue empleado en el 23 % de las tareas. Sin embargo, hubo variaciones a través del tiempo (Gráfica 7), distinguiéndose dos etapas. El sistema verbal-simbólico ronda el 90 % en casi todos los periodos hasta el 2018, luego empieza a disminuir en comparación con el crecimiento de la frecuencia de uso del sistema múltiple, el cual llega a su porcentaje mayor (53 %) en el segundo periodo del 2020 y se mantiene en el 50 % en los periodos siguientes (excepto en el segundo periodo del 2021).

Gráfica 7. Distribución porcentual de tareas por periodo, según representación

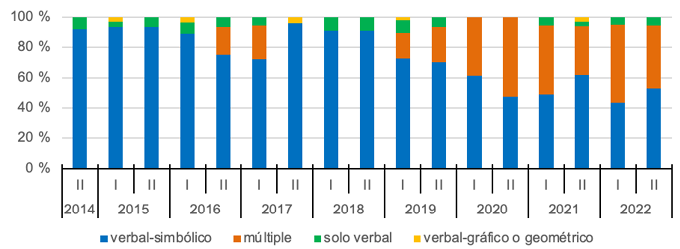
Nota: fuente propia de la investigación.

Finalmente, sobre la situación en que se proponen las tareas, la situación científica exclusivamente matemática predomina, tanto a nivel general (94 %) como a lo largo del tiempo (Gráfica 8), destacándose el segundo periodo del 2015, cuando fue el único tipo de situación propuesta. En menor medida se hizo referencia a situaciones científico-tecnológicas no exclusivamente matemáticas, presentes en el 6 % del total de tareas analizadas, destacándose el primer periodo del 2019 como el de mayor uso (13 %).

Gráfica 8. Distribución porcentual de tareas por periodo, según situación

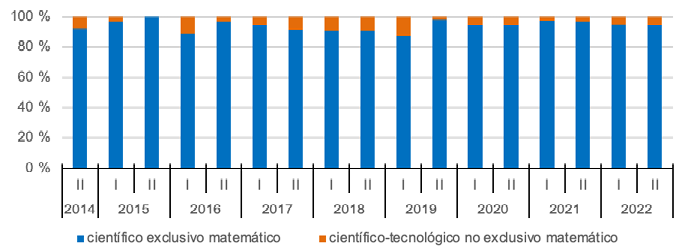
Nota: fuente propia de la investigación.

En resumen, los resultados de este apartado, sobre los significados del contenido matemático en las tareas evaluadas, muestran que en general hay amplia variedad de contenidos específicos por unidad de contenido y predominan la representación verbal-simbólica y la situación científica exclusivamente matemática. Este predominio fue constante a lo largo del tiempo, mientras que, en la representación verbal-simbólica tendió a disminuir a favor de la representación múltiple, hasta equilibrarse.

Por su parte, algunos contenidos específicos estuvieron presentes a lo largo del tiempo (regla de L´Hopital, límite al infinito, continuidad, áreas, integral indefinida por sustitución trigonométrica), otros en periodos específicos (interpretación gráfica de la primera derivada, límite unilateral, derivación por teoremas, rectas tangente y normal, derivada de orden superior, derivación implícita, integral indefinida por sustitución, por fracciones parciales y por partes), mientras otros tuvieron escaza presencia (interpretación gráfica de la segunda derivada, límite por teorema del encaje, teorema de Rolle).

Además, algunas de las variaciones en el tiempo coinciden con la etapa de pandemia por Covid-19, entre ellas: la presencia de contenidos específicos como interpretación gráfica de la primera y segunda derivada y disminución del sistema de representación verbal-simbólica a favor del múltiple.

Aspectos cognitivos de las tareas matemáticas evaluadas

En relación con los aspectos cognitivos, se analizó demanda, acción, dirección y relación requeridas para realizar cada tarea. En cuanto a la demanda cognitiva prevista, según las características de los procesos implicados al realizar las tareas, predominan los procedimientos sin conexiones (68 %), seguida de procedimientos con conexiones (24 %) y hacer matemática (7 %).

Sin embargo, hubo variaciones a través del tiempo (Gráfica 9). En los casos de procedimientos con y sin conexiones, se distinguen tres etapas. Primero, los procedimientos sin conexiones rondan el 70 % en casi todos los periodos hasta el primer periodo del 2020. Luego, en el segundo periodo del 2020 y el primero del 2021, los procedimientos con conexiones aumentan su frecuencia de aparición (50 % y 57 %, respectivamente). Por último, del segundo periodo del 2021 en adelante, los procedimientos con conexiones disminuyen de forma paulatina, pasando de 41 % (segundo periodo del 2021) a 31 % y 24 % (primer y segundo periodo del 2022, respectivamente).

Gráfica 9. Distribución porcentual de tareas por periodo, según demanda

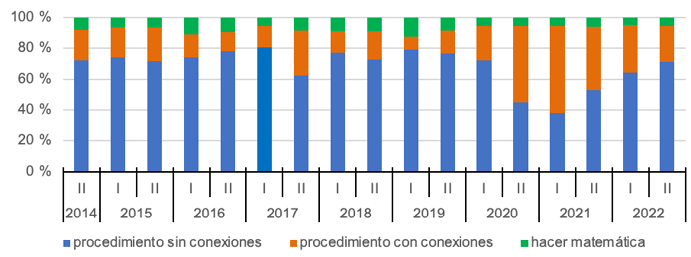
Nota: fuente propia de la investigación.

Sobre la acción requerida explícitamente indicada en el enunciado de la tarea, predominan “determinar” (44 %) y “calcular” (38 %), seguidas de “resolver” (7 %). Sin embargo, hubo ciertas variaciones a través del tiempo (Gráfica 10). Por ejemplo, “determinar” sobrepasa el 50 % en cada periodo del 2020 en adelante, mientras que “calcular” se ve disminuida en comparación con los periodos anteriores. Por su parte, las acciones “usar” y “trazar” solo aparecen en los primeros periodos, e “identificar” en los últimos. Además, algunas acciones únicamente se encontraron en pocos periodos de forma aislada (“explicar”, “justificar” y “verificar”).

Gráfica 10. Distribución porcentual de tareas por periodo, según acción

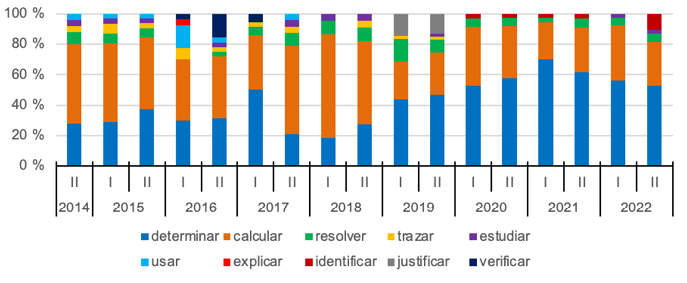
Nota: fuente propia de la investigación.

En lo concerniente a la dirección prevista en que se deben realizar las acciones para determinar lo solicitado en las tareas, predomina el rumbo directo, utilizado en el 76 % del total de tareas analizadas. Mientras que el rumbo inverso corresponde al 24 % restante. Sin embargo, se presentaron variaciones a través del tiempo (Gráfica 11), distinguiéndose tres etapas. En casi todos los periodos hasta el primer periodo del 2020, el rumbo directo ronda el 85 %. Luego, en el segundo periodo del 2020 y el primer periodo del 2020, el rumbo inverso aumenta su frecuencia de aparición, llegando a un equilibro entre ambos. Finalmente, del segundo ciclo del 2021 en adelante, el rumbo inverso disminuye su frecuencia, pero no alcanza el mismo grado que en la fase previa al equilibro, pues permanece cerca del 30 %.

Gráfica 11. Distribución porcentual de tareas por periodo, según dirección

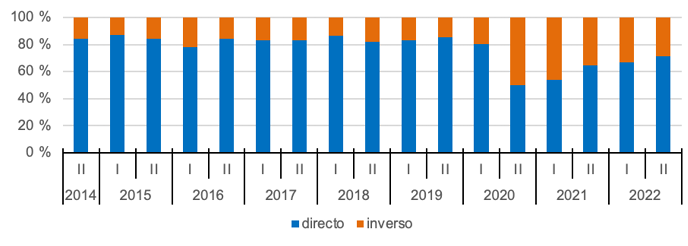
Nota: fuente propia de la investigación.

En lo que se refiere a la relación de cada tarea con el resto de las tareas del mismo examen, el 36 % corresponde a relaciones “solamente de información” (función matemática o datos implicados), seguidas de relaciones “nulas” (32 %), “solamente de enunciado” (28 %) y de “solución e información” (5 % restante). Sin embargo, las múltiples variaciones a través del tiempo (Gráfica 12), no muestran algún tipo de relación predominante. Se distinguen cuatro etapas. Primero, la relación “solamente de enunciado” predomina rondando el 50 % en casi todos los periodos hasta el segundo periodo del 2018. En el 2019, las relaciones “solamente de información” y “nula” aumentan su frecuencia de aparición, llegando a rondar el 85 % (entre ambas) en el segundo periodo del 2019. Esa tendencia de crecimiento continua en el 2020 y 2021, cuando entre ambas alcanzan el 100 % (“nula” ronda el 60 % y “solamente información” el 40 %). Finalmente, en el 2022, la relación “solamente de información” aumenta su presencia (ronda el 55 %), la relación “nula” disminuye de forma considerable (ronda el 8 %) y reaparece la relación “solamente de enunciado” (ronda el 35 %).

Gráfica 12. Distribución porcentual de tareas por periodo, según relación

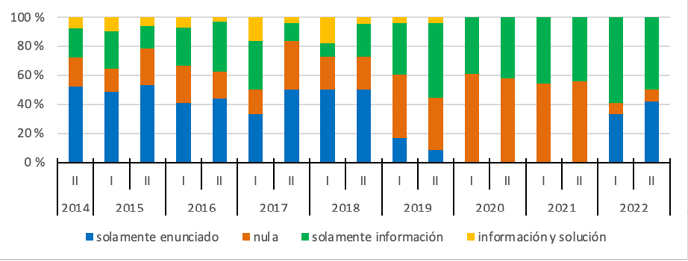
Nota: fuente propia de la investigación.

En resumen, los resultados de este apartado, sobre aspectos cognitivos en las tareas evaluadas, muestran que en general prevalecen la demanda cognitiva procedimientos sin conexiones y el rumbo directo, mientras que las acciones y relaciones presentan variedad. A lo largo del tiempo, la preferencia tanto de la demanda cognitiva procedimientos sin conexiones como del rumbo directo tendió a disminuir a favor de los procedimientos con conexiones y del rumbo inverso, respectivamente. A su vez, algunas acciones y relaciones estuvieron presentes a lo largo del tiempo (acciones: determinar, calcular y resolver; relaciones: solamente de información y nula), otras en periodos específicos (acciones: usar, trazar e identificar; relación: información y solución), mientras otras tuvieron escaza presencia (acciones: explicar, justificar y verificar).

Además, algunas de las variaciones a través del tiempo coinciden con la etapa de pandemia por Covid-19, entre ellas: la disminución de la demanda cognitiva en procedimientos sin conexiones a favor de procedimientos con conexiones, y la reducción del rumbo directo a favor del rumbo inverso. En ambos casos, la tendencia retrocedió después de la etapa de pandemia, de mayor (demanda cognitiva) a menor medida (dirección).

Discusiones y conclusiones

El estudio se enfocó en realizar una caracterización didáctica e histórica de tareas matemáticas evaluadas en exámenes universitarios de cálculo. Para ello, se analizaron aspectos sobre el significado de los contenidos matemáticos y aspectos cognitivos. Además, se examinó la evolución de estos rasgos a través del tiempo.

En términos generales, se observó que las tareas matemáticas en los exámenes tienden a subestimar la naturaleza compleja del pensamiento matemático requerido para la comprensión del cálculo. Estas tareas se centran en contenidos y habilidades técnicas, lo cual refleja parcialmente algunos aspectos fundamentales del significado de los contenidos matemáticos y aspectos cognitivos del aprendizaje; pues, aunque hay variedad de contenidos, predominan ciertos rasgos particulares, como la representación verbal-simbólica, la situación científica exclusivamente matemática, la demanda cognitiva de procedimientos sin conexiones y el rumbo directo.

Estas características coinciden con hallazgos de otros estudios que también han destacado el equilibrio de contenidos, además del predominio de formulaciones verbales-simbólicas, situaciones meramente matemáticas y razonamientos algorítmicos instrumentales de reproducción (Caraballo et al., 2011; Bhaird et al., 2017; Ruiz-Hidalgo et al., 2019; Gaona y Vivier, 2022). Sin embargo, estas características, contradicen la insistente recomendación de diversificar estas tareas en términos de: (a) sistemas de representación y conversiones entre sistemas (Castro y Castro, 1997; Lupiáñez, 2016), (b) situaciones y contextos, matemáticos y extramatemáticos, que aporten sentido respecto a para qué se usa un contenido matemático (NCTM, 1995; Ruiz-Hidalgo, 2016; Swan y Burkhardt, 2012; Van den Heuvel-Panhuizen y Becker, 2003; Watson y Ohtani, 2015) y (c) demandas cognitivas que involucren altos niveles de pensamiento y razonamiento (Smith y Stein, 1998; Swan y Burkhardt, 2012; Ruiz-Hidalgo y Rico, 2016).

A pesar de estas tendencias, el enfoque histórico de este estudio permitió identificar características de las tareas que variaron a través del tiempo o que permanecieron constantes. Por una parte, el predominio de las situaciones científicas exclusivamente matemáticas fue constante a través del tiempo, confirmándose que este aspecto requiere de atención, pues se está lejos de lo recomendado. Por otra parte, ciertos rasgos mostraron un acercamiento a lo sugerido, pues, a partir de cierto periodo, la representación verbal-simbólica, los procedimientos sin conexiones y el rumbo directo tendieron a disminuir a favor de la representación múltiple, los procedimientos con conexiones y el rumbo inverso, respectivamente. Es importante destacar que estas variaciones coincidieron con el uso de exámenes en línea durante la etapa de la pandemia por Covid-19, pero persistieron o retrocedieron ligeramente cuando se retomaron los exámenes presenciales en papel y lápiz.

Si bien, el enfoque principal de este estudio fue la caracterización de las tareas matemáticas evaluadas en los exámenes, también se examinaron los sistemas utilizados para analizar los exámenes y sus tareas. Resultó que predominan los exámenes parciales aplicados a lo largo del curso, diseñados y calificados por el personal docente para evaluar contenidos con el único propósito (explícitamente declarado en los programas de estudio) de determinar la promoción a través de una calificación, en la cual los exámenes tuvieron un peso significativo. Sin embargo, se observaron algunas variaciones a través del tiempo. Varias de ellas coincidieron con la etapa de pandemia por Covid-19 y se mantuvieron (inclusión de métodos de evaluación complementarios) o retrocedieron (evaluaciones en línea) posteriormente.

Sobre los sistemas de evaluación empleados en el curso se destacan algunos aspectos. En primer lugar, la falta de enfoque en objetivos de aprendizaje o competencias en lugar de contenidos (Sánchez, 2011). En segundo lugar, el énfasis en los exámenes escritos con un peso significativo en la calificación y dejando de lado la aplicación en línea, a pesar de las ventajas potenciales de los enfoques plurales de evaluación (NCTM, 1995; Sánchez, 2011) y del uso de la tecnología en la evaluación: resultados en tiempo real, facilidad de administración de datos, menor tiempo para calificar, posibilidad de individualización aun con grupos numerosos, constante actualización de las tecnologías, múltiples registros de experiencias y uso cada vez más generalizado (Miller, 2009; Sangwin, 2013; Terzis et al., 2012).

En tercer lugar, la falta de referencias a autoevaluación o coevaluación, cuando estos elementos, junto con la retroalimentación efectiva y los procesos autorregulatorios del aprendizaje, son fundamentales en los enfoques modernos de evaluación en la enseñanza: evaluación formativa (Black y William, 1998; Sadler, 1989) y evaluación para el aprendizaje (De la Orden y Pimienta, 2016; Stiggings, 2014). En último lugar, que el único propósito de la evaluación declarado explícitamente sea dar una calificación y determinar la promoción, cuando existen múltiples propósitos por los cuales se evalúa: determinar intervenciones, mejorar los procesos de enseñanza-aprendizaje, identificar dificultades u obstáculos, retroalimentar, autorregular el aprendizaje o diagnosticar (Suurtamm et al., 2016). Es fundamental tener claro para qué se evalúa y qué se promueve (Moreno-Olivos, 2010), pues el propósito delimita otras dimensiones (método, momento, sujeto) y distingue diferentes enfoques de evaluación (Suurtamm et al., 2016). Por ejemplo, evaluación sumativa para la selección, clasificación, promoción y certificación de logros, y evaluación formativa para la aproximación de la enseñanza del profesorado a los logros de aprendizaje de sus estudiantes a través de la retroalimentación (De la Orden y Pimienta, 2016).

Dado que se anticipa que los exámenes seguirán siendo relevantes en las prácticas de evaluación en educación matemática (Suurtamm et al., 2016), y al considerar que las tareas matemáticas evaluadas en estos exámenes a menudo representan el punto máximo de aprendizaje alcanzado en la mayoría de las aulas (Swan y Burkhardt, 2012), es esencial reconocer que el diseño adecuado de estas tareas tiene un potencial significativo para impulsar mejoras en la calidad de la educación (Swan y Burkhardt, 2012). Por lo tanto, es crucial prestar atención a las características didácticas de las tareas matemáticas utilizadas en la evaluación y su evolución histórica.

Algunas cuestiones que podrían abrir nuevas vías en el estudio de las tareas matemáticas de evaluación: (a) comparar evaluaciones diseñadas por docentes para sus estudiantes, en particular con pruebas a gran escala aplicadas por igual a todos los grupos de estudiantes, (b) analizar las experiencias del cuerpo docente en relación con la evaluación, basándose en sus propios relatos, (c) estudiar la diferencia entre las tareas matemáticas evaluadas en línea y las tareas en exámenes a papel y lápiz, (d) evaluar cómo las experiencias durante la pandemia por Covid-19 han influido en las prácticas de evaluación posteriores a la pandemia y (e) analizar las prácticas de evaluación en cursos convencionales de cálculo en diferentes contextos. Estas nuevas perspectivas tienen el potencial de generar nuevos hallazgos y enriquecer la comprensión general de este tema.

Conflicto de intereses

Las personas autoras declaran no tener algún conflicto de interés.

Declaración de la contribución de las personas autoras

Todas las personas autoras afirmamos que se leyó y aprobó la versión final de este artículo.

El porcentaje total de contribución para la conceptualización, preparación y corrección de este artículo fue el siguiente: M. G. C. T. 50 %, J. F. R. H. 50 %.

Declaración de disponibilidad de los datos

Los datos que respaldan los resultados de este estudio serán puestos a disposición por el autor o la autora correspondiente [M. G. C. T.], previa solicitud razonable.

Preprint

Una versión Preprint de este artículo fue depositada en: https://dx.doi.org/10.2139/ssrn.4564010

Referencias

Askew, M., Hodgen, J., Hossain, S. y Bretscher, N. (2010). Values and variables: Mathematics education in high-performing countries. Nuffield Foundation.

Balcaza, T., Contreras, A. y Font, V. (2017). Análisis de Libros de Texto sobre la Optimización en el Bachillerato. Bolema, 31(59), 1061-1081. https://doi.org/10.1590/1980-4415v31n59a11

Bhaird, C. M., Nolan, B. C., O’Shea, A. y Pfeiffer, K. (2017). A study of creative reasoning opportunities in assessments in undergraduate calculus courses. Research in Mathematics Education, 19(2), 147-162. https://doi.org/10.1080/14794802.2017.1318084

Black, P. y Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education, 5(1), 7-74. http://dx.doi.org/10.1080/0969595980050102

Caraballo, R. M., Rico, L. y Lupiáñez, J. L. (2011). Análisis de los ítems de las evaluaciones autonómicas de diagnóstico en España 2008-2009. Unión: Revista Iberoamericana de Educación Matemática, 7(26), 27-40. http://www.revistaunion.org/index.php/UNION/article/view/925

Castro, E. y Castro, E. (1997). Representaciones y modelización. En L. Rico (Ed.), La educación matemática en la enseñanza secundaria (pp. 95-124). Horsori.

Cohen, L., Manion, L. y Morrison, K. (2017). Research methods in education. Routledge. https://doi.org/10.4324/9781315456539

De la Orden, A. y Pimienta, J. H. (2016). Instrumento para determinar los tipos de evaluación utilizados por los profesores universitarios. Revista Electrónica de Investigación Educativa, 18(2), 40-52. http://redie.uabc.mx/redie/article/view/1088

Fernández-Plaza, J. A. (2016). Análisis de contenido. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 103-118). Ediciones Pirámide.

Flores, P. y Lupiáñez, J. L. (2016). Expectativas de aprendizaje. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 177-194). Ediciones Pirámide.

Gaona, J. y Vivier, L. (2022). Valor Epistémico de Tareas Diseñadas en un Sistema de Evaluación en Línea con Retroalimentación para Matemáticas. Revista de Matemática, Ensino e Cultura - REMATEC, 17(42), 79-110. https://doi.org/10.37084/REMATEC.1980-3141.2022.n42.p111-138.id453

García-Oliveros, G., Salguero-Rivera, B., Rodríguez-Díaz, O., Palomino-Bejarano, E. y Caicedo-Valencia, R. (2020). Las prácticas de evaluación de las matemáticas universitarias: Tensiones y desafíos desde la red conceptual en la que se inscriben. Uniciencia, 34(1), 246-262. http://dx.doi.org/10.15359/ru.34-1.14

Krippendorff, K. (2019). Content analysis: An introduction to its methodology. Sage publications. https://doi.org/10.4135/9781071878781

Lupiáñez, J. L. (2016). Sistemas de representación. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 119-138). Ediciones Pirámide.

Martinez-Luaces, V., Rico, L., Fernández-Plaza, J. A. y Ruiz-Hidalgo, J. F. (2018). Enriquecimiento de tareas y problemas de modelado inverso: Una experiencia con profesores en formación. En L. J. Rodríguez-Muñiz, L. Muñiz-Rodríguez, A. Aguilar-González, P. Alonso, F. J. García García y A. Bruno (Eds.), Investigación en Educación Matemática XXII (pp. 320-329). SEIEM. https://www.seiem.es/docs/actas/22/ActasXXIIDefinitivas.pdf

Miller, T. (2009). Formative computer-based assessment in higher education: the effectiveness of feedback in supporting student learning. Assessment & Evaluation in Higher Education, 34(2), 181-192. http://doi.org/10.1080/02602930801956075

Ministerio de Educación Pública [MEP]. (2012). Programas de Estudio de Matemáticas. MEP. https://www.mep.go.cr/programa-estudio/matematicas

Ministerio de Educación y Formación Profesional. (2022), Real Decreto 243/2022, de 5 de abril, por el que se establecen la ordenación y las enseñanzas mínimas del Bachillerato. Boletín Oficial del Estado, 82, 46047-46408. https://www.boe.es/eli/es/rd/2022/04/05/243/con

Moreno, A. y Ramírez, R. (2016). Variables y funciones de las tareas matemáticas. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 243-257). Ediciones Pirámide.

Moreno-Olivos, T. (2010). Lo bueno, lo malo y lo feo: las muchas caras de la evaluación. Revista Iberoamericana de Educación Superior, 2(1), 84-97. https://doi.org/10.22201/iisue.20072872e.2010.2.6

National Council of Teachers of Mathematics [NCTM]. (1995). Assessment standards for school mathematics. NCTM.

National Council of Teachers of Mathematics [NCTM]. (2000). Principles and Standards for School Mathematics. NCTM.

National Governors Association Center for Best Practices and Council of Chief State School Officers [NGA y CCSSO]. (2010). Common Core State Standards for Mathematics. NGA y CCSSO.

Organization for Economic Co-operation and Development [OECD]. (2016). PISA 2015 Assessment and Analytical Framework: Science, Reading, Mathematics and Financial Literacy. PISA, OECD Publishing. https://doi.org/10.1787/9789264255425-en

Ramos, L. y Casas, L. (2018). Demanda Cognitiva de Estándares Educativos y Libros de Texto para la Enseñanza del Álgebra en Honduras. Bolema, 32(62), 1134-1151. https://doi.org/10.1590/1980-4415v32n62a19

Rico, L. (1997a). Bases teóricas del currículo de matemáticas en educación secundaria. Síntesis.

Rico, L. (1997b). Los organizadores del currículo de matemáticas. En L. Rico (Ed.), La educación matemática en la enseñanza secundaria (pp. 39-59). Horsori.

Rico, L. (2013). El método del Análisis Didáctico. Unión: Revista Iberoamericana de Educación Matemática, 9(33), 11-27. https://revistaunion.org/index.php/UNION/article/view/801

Rico, L. (2016). Matemáticas y análisis didáctico. En L. Rico y A. Romero (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 85-100). Ediciones Pirámide.

Rico, L. y Fernández-Cano, A. (2013). Análisis didáctico y metodología de investigación. En L. Rico, J. L. Lupiáñez y M. Molina (Eds.), Análisis Didáctico en Educación Matemática: metodología de investigación, formación de profesores e innovación curricular (pp. 1-22). Editorial Comares.

Rico, L. y Moreno, A. (Eds.). (2016). Elementos de didáctica de la matemática para el profesor de secundaria. Ediciones Pirámide.

Rico, L. y Ruiz-Hidalgo, J. F. (2018). Ideas to work for the curriculum change in school Mathematics. En Y. Shimizu y R. Vithal (Eds.), Conference proceedings of the twenty-fourth ICMI Study: School Mathematics curriculum reforms: Challenges, changes and opportunities (pp. 301-308). Tsukuba, Japan: International Commission on Mathematical Instruction and University of Tsukuba. https://www.researchgate.net/publication/334548491_Ideas_to_work_for_the_curriculum_change_in_school_Mathematics

Rico, L., Lupiáñez, J. L. y Molina, M. (Eds.). (2013). Análisis Didáctico en Educación Matemática: metodología de investigación, formación de profesores e innovación curricular. Editorial Comares.

Ruiz-Hidalgo, J. F. (2016). Sentidos y modos de uso de un concepto. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de Secundaria (pp. 139-151). Ediciones Pirámide.

Ruiz-Hidalgo, J. F., Herrera Beltrán, M. E. y Velasco, M. V. (2019). Tareas de Cálculo en las pruebas de acceso a la Universidad. Revista de educación, (386), 137-164. https://doi.org/10.4438/1988-592X-RE-2019-386-430

Ruiz-Hidalgo, J. F. y Rico, L. (2016). Oportunidades para el aprendizaje. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 209-224). Ediciones Pirámide.

Sadler, D. R. (1989). Formative assessment and the design of instructional systems. Instructional Science, 18, 119-144. https://doi.org/10.1007/bf00117714

Sánchez, J. (2011). Evaluación de los aprendizajes universitarios: una comparación sobre sus posibilidades y limitaciones en el Espacio Europeo de Educación Superior. Revista de Formación e Innovación Educativa Universitaria, 4(1), 40-54. https://www.researchgate.net/publication/268401009

Sangwin, Ch. (2013). Computer Aided Assessment of Mathematics. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199660353.001.0001

Segovia, I. (2016). Evaluación en matemáticas. En L. Rico y A. Moreno (Eds.), Elementos de didáctica de la matemática para el profesor de secundaria (pp. 309-328). Ediciones Pirámide.

Segovia, I. y Rico, L. (2001). Unidades didácticas: organizadores. En E. Castro (Ed.), Didáctica de la matemática en la Educación Primaria (pp. 83-104). Síntesis.

Smith, M. S. y Stein, M. K. (1998). Reflection on practice: Selecting and creating mathematical tasks: From research to practice. Mathematics teaching in the middle school, 3(5), 344-350. https://doi.org/10.5951/MTMS.3.5.0344

Soh, C. K. (2008). An overview of mathematics education in Singapore. En Z. Usiskin y E. Willmore (Eds.), Mathematics Curriculum in Pacific Rim Countries (pp. 23-36). Information Age Publishing.

Stein, M. K., Grover, B. W. y Henningsen, M. (1996). Building Student Capacity for Mathematical Thinking and Reasoning: An Analysis of Mathematical Tasks Used in Reform Classrooms. American Educational Research Journal, 33(2), 455-488. https://doi.org/10.3102/00028312033002455

Stiggings, R. (2014). Revolutionize assessment. Empower students, inspire learning. Corwing.

Suurtamm, C., Thompson, D. R., Kim, R. Y., Moreno, L. D., Sayac, N., Schukajlow, S., Silver, E., Ufer, S. y Vos, P. (2016). Assessment in mathematics education. Springer. https://doi.org/10.1007/978-3-319-32394-7

Swan, M. y Burkhardt, H. (2012). A designer speaks: designing assessment of performance in mathematics. Educational Designer: Journal of the International Society for Design and Development in Education, 2 (5), 1-41. https://www.educationaldesigner.org/ed/volume2/issue5/article19/

Terzis, V., Moridis, C. N. y Economides, A. A. (2012). The effect of emotional feedback on behavioral intention to use computer based assessment. Computers & Education, 59(2), 710-721. http://doi.org/10.1016/j.compedu.2012.03.003

Van den Heuvel-Panhuizen, M. y Becker, J. (2003). Towards a didactic model for assessment design in mathematics education. En A. Bishop, M. Clements, C. Keitel, J. Kilpatrick y F. Leung (Eds.), Second International Handbook of Mathematics Education (pp. 689-716). Kluwer Academic Publishers. https://doi.org/10.1007/978-94-010-0273-8_23

Vargas, M. F., Fernández-Plaza, J. A. y Ruiz-Hidalgo, J. F. (2020). Significado de derivada en las tareas de los libros de 1° de Bachillerato. Bolema: Boletim de Educação Matemática, 34(68), 911-933. https://doi.org/10.1590/1980-4415v34n68a04

Watson, A. y Ohtani, M. (Eds.) (2015). Task design in mathematics education: An ICMI study22 (p. 339). Springer Nature. https://doi.org/10.1007/978-3-319-09629-2

White, N. y Mesa, V. (2014). Describing Cognitive Orientation of Calculus I Tasks Across Different Types of Coursework. ZDM: International Journal on Mathematics Education, 46(4), 675-690. https://doi.org/10.1007/s11858-014-0588-9

---

1. 1* Corresponding author

   María G. Calderón-Torres, maria.calderon.torres@una.ac.cr, https://orcid.org/0000-0002-2877-8899

   Juan F. Ruiz- Hidalgo, jfruiz@ugr.es, https://orcid.org/0000-0002-4805-6922

   Escuela de Matemática, Universidad Nacional, Heredia, Costa Rica.

1. 2 Departamento de Didáctica de la Matemática, Universidad de Granada, Granada, España.