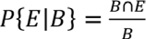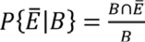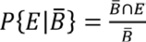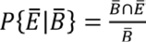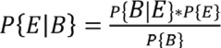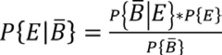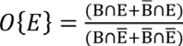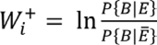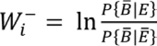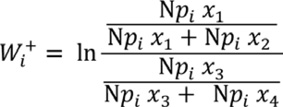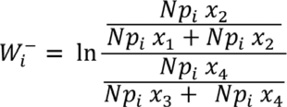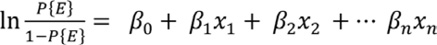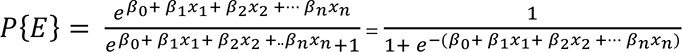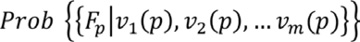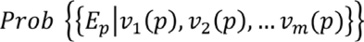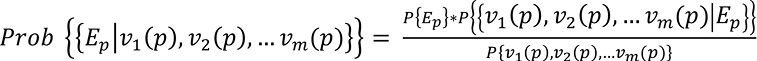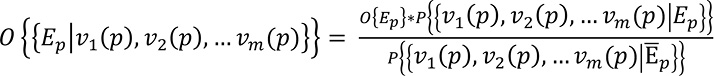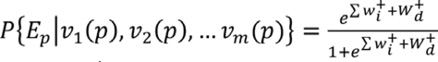Revista de Ciencias Ambientales (Trop J Environ Sci). (Enero-Junio, 2018). EISSN: 2215-3896. Vol 52(1): 1-26.

DOI: http://dx.doi.org/10.15359/rca.52-1.1

URL: www.revistas.una.ac.cr/ambientales

EMAIL: revista.ambientales@una.cr

---

Análisis espacial de susceptibilidad de erosión en una cuenca hidrográfica del trópico húmedo de Costa Rica

Erosion Susceptibility Assessment using Statistical Models at a Tropical Watershead in Costa Rica

Iván Pérez-Rubioa, Andreas Mendeb

[Recibido: 4 de julio 2017. Aceptado: 3 de octubre 2017. Corregido: 8 de noviembre 2017. Publicado: 01 de enero 2018]

Resumen El objetivo del presente estudio consiste en evaluar el estado de conservación de una cuenca hidrográfica en el trópico húmedo de Costa Rica en términos de su capacidad de proveer el servicio ecosistémico para control de la erosión. Mediante la interpretación de fotografías aéreas del proyecto CARTA (2005) se realizó primeramente un inventario espacial de los procesos erosivos observables en el área de estudio. Se parte del supuesto de que su distribución espacial no es aleatoria sino que depende de la interacción compleja de factores naturales y antrópicos. Para evaluar cuantitativamente dicha relación espacial se planteó un análisis de susceptibilidad de erosión. Se aplicó dos métodos comparativos: 1) regresión logística binaria y 2) probabilidad condicional conjunta, mediante el teorema de Bayes. Ambas alternativas se combinaron con un análisis estadístico bivariado basado en el cálculo de las ponderaciones de evidencia (weights of evidence) de todas las clases de los factores condicionantes incorporados en el modelo: el uso del suelo, la pendiente, la geomorfología y la distancia a la red de drenaje. Los resultados de los cálculos de las ponderaciones de evidencia y la interpretación de los coeficientes de la ecuación de regresión logística demostraron la relevancia relativa dominante del factor uso del suelo sobre la geomorfología. Los mapas de susceptibilidad resultantes fueron evaluados mediante dos procedimientos de verificación, en primer lugar, la curva del ratio de acierto (success rate) y la función ROC (Receiver Operating Characteristic); en ambos casos el método de probabilidad conjunta mostró un mayor nivel de precisión que el de regresión logística. Palabras clave: ponderaciones de evidencia, regresión logística binaria, probabilidad condicional conjunta, curva ROC, Sistemas de Información Geográfica (SIG). Abstract The aim of this study is to assess the state of conservation of a tropical watershead in Costa Rica in terms of its capacity to provide the ecossytem service of control of erosion. Firstly a spatial inventory of erosion occurrence areas was made by the interpretation of aerial photographs (CARTA Project). It was previously made under the condition that its spatial distribution is not random but depends on the complex interaction of natural and human factors. The methodology applied to quantify that spatial relationship was based on the stadistical analysis of erosion susceptibility. To do that it were applied two comparative methods: 1) a multivariate logistic regression and 2) a joint condicional probability model under Bayesian theorem. The two alternatives were combined with an indirect bivariate statistical analysis base on the weights of evidence method. The positive weight of evidence was assigned to each of the different classes into which a factor map is classified: land use, the slope gradient, geomorphology, and distance to streams. The results of the calculation of the weights of evidence and the interpretation of the coeficientes of the ecuation of logistic regression demostrated that the most relevant factor map was the land use. The both susceptibility maps were evaluated through two different methodologies: the success rate and the ROC curve. The validation results revealed that the joint conditional model was slightly better at predicting erosion features than the logistic regression model. Keywords: weights of evidence modelling, multivariate logistic regression, joint conditional probability, ROC curve, Geographical Information Systems (SIG).

1. Introducción

La erosión del suelo es considerada como uno de los problemas más graves, desde un punto de vista ecológico y económico, que enfrentan los países tropicales (Bayard et al., 2006). Según la FAO (1984) la erosión hídrica es la forma más común de erosión, que provoca enormes daños y desastres por inestabilidad de las laderas.

Uno de los factores antrópicos generadores de incrementos dramáticos de erosión del suelo y producción de sedimentos es la deforestación de los bosques nativos en las cuencas hidrográficas tropicales (Bosh y Hewlett 1982; Gilmour, 1977; Falkenmark y Chapman, 1989; Fritsch, 1993; Douglas, 1996; Kiersch, 2000; Bruijnzeel, 2004). Esta tendencia incluso se acelera en terrenos próximos a apertura de trochas y tránsito de tractores (Riijsdijk y Bruijnzeel, 1991; Purwanto, 1999; Calder, 2002).

En América Latina y el Caribe la ganadería es uno de los principales usos del suelo; en Centroamérica cerca de 48 % de su extensión se utiliza para pastoreo (Steinfeld, 2002); nueve millones del total de hectáreas fueron transformadas de bosque a pasturas y monocultivos, las cuales presentan un alto nivel de degradación de suelos (Szott et al., 2000; Stocking y Murnaghan, 2003).

En América Central, el sobrepastoreo ha provocado que más del 50 % de las tierras en laderas se encuentren con algún grado de degradación del suelo (Kaimowitz, 1996). En zonas tropicales deforestadas y con altas precipitaciones, el pastoreo es responsable de la formación de cárcavas y tiende a hacer que el suelo se compacte dando como resultado una reducción de la infiltración y acelerada erosión (Chomitz y Kumari, 1996; Bruijnzeel, 2004), sobre todo cuando esta actividad se desarrolla en terrenos con pendiente fuerte (Arce, 2004).

Existen diferentes métodos cuantitativos tanto determinísticos como estadísticos que permiten zonificar las áreas más propensas a sufrir procesos de erosión. En los estudios estadísticos se pueden utilizar modelos de susceptibilidad (susceptibility) o modelos de medición del riesgo o amenaza (hazard). Ambos modelos se diferencian en que estos últimos incluyen tanto los factores llamados condicionantes, que son variables intrínsecas del terreno, entre ellas: el uso del suelo, pendiente, geología, geomorfología, etc., como los factores activadores, variables extrínsecas, tales como las precipitaciones o las fallas tectónicas (Van Westen et al., 2003).

En los modelos de susceptibilidad y en los de amenaza se emplean diferentes herramientas estadísticas, que incluyen: 1) las ponderaciones de evidencia, en los llamados modelos estadísticos bivariados (Van Westen, 1993; Van Westen et al., 2003), 2) regresión lineal multivariada (Carrara et al., 1991; Chung et al., 1995), 3) regresión logística binaria (Chung y Fabbri, 1999; Dai y Lee, 2002; Lee, 2005; Ayalew y Yamagishi, 2005; Pineda et al., 2011; Akbari et al., 2014; Lee et al., 2016), 4) probabilidad condicional conjunta mediante el teorema de Bayes (Chung y Fabbri, 1999). Más recientemente se han introducido nuevos enfoques como la evaluación multicriterio espacial (Castellanos y Van Westen, 2007; Pourgashemi et al., 2012; Shahabi y Hashim, 2015), las redes neuronales (Pradhan y Lee, 2010), y la lógica difusa (fuzzy logic) (Pradhan, 2010).

A diferencia de los estudios anteriores en los cuales se analizan específicamente los deslizamientos del terreno, el presente trabajo se planteó como un análisis espacial de susceptibilidad aplicado sobre procesos genéricos de erosión con el propósito de evaluar el estado de conservación de la cuenca hidrográfica. Para ello se empleó dos métodos de análisis estadístico multivariado: 1) regresión logística binaria y 2) probabilidad condicional conjunta mediante la fórmula de Bayes. Ambos métodos estadísticos se complementan con un análisis estadístico bivariado mediante el cálculo de las ponderaciones de evidencia (weights of evidence) (Bonham-Carter, 1994; Van Westen et al., 2003) que permite determinar el grado de relevancia de cada una de las clases en que se subdivide cada factor, comparando la densidad de procesos de erosión dentro del área de cada clase con la densidad en toda el área de estudio (Bonham-Carter, 1994).

2. Metodología

2.1. Área de estudio

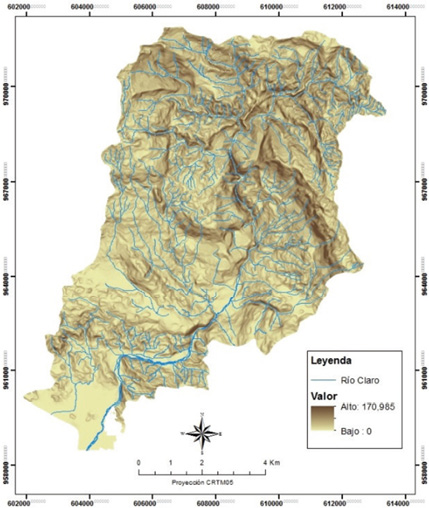
El área de estudio abarca una extensión de 100,81 km² y un perímetro de 62,27 km correspondientes a la subcuenca hidrográfica del río Claro que forma parte de la Fila Cruces, en el Pacífico Sur de Costa Rica, distrito de Guaycará, cantón de Golfito y provincia de Puntarenas. La subcuenca se localiza entre las coordenadas geográficas 8º 40’ – 8º 47’ 30’’ latitud norte y 82º 57’ 30’’ – 83º 4’ 30’’ longitud oeste.

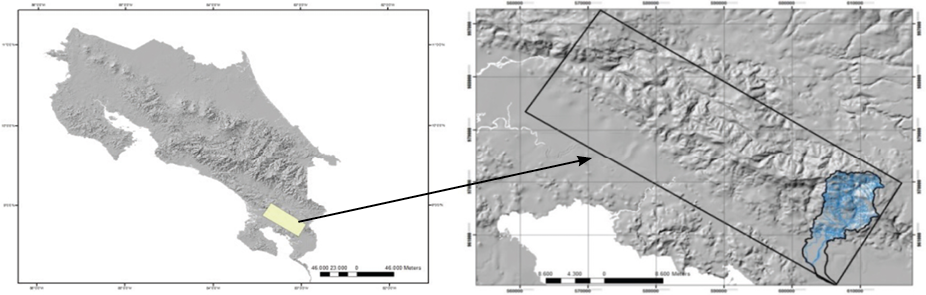
Figura 1. Localización geográfica del área de estudio, cuenca hidrográfica del río Claro

El clima del área de estudio es tropical muy húmedo, con una estación seca corta (con menos de 35 días sin lluvias) desde la última semana de enero hasta mediados de abril. Una temperatura media anual entre 23-27 °C; la precipitación media anual varía entre 2 840-6 840 mm (Herrera, 1986). La Fila Cruces se orienta de noroeste a sureste paralela a la costa del Océano Pacífico (Figura 1), la máxima elevación es el cerro Anguciana, con 1 707 m.s.n.m. Los suelos son ultisoles (suelo rojizo, profundo, arcilloso y ácido) en el piedemonte de la Cordillera e inceptisoles en áreas montañosas (Pérez et al., 1978). Ecológicamente es una zona de alto endemismo debido a los procesos geológicos y evolutivos (Valerio, 1998; Lobo y Bolaños, 2005; Riba, 2007).

El ecosistema posee un gran valor ambiental al albergar los cursos de agua más importantes de las principales subcuencas de la cuenca del Golfo Dulce (Lobo y Bolaños, 2005). Sin embargo, estos aspectos positivos se encuentran bajo una amenaza exponencialmente creciente debido a los procesos de deforestación y fragmentación que han sido ocupadas principalmente por ganadería extensiva y una agricultura de subsistencia que en determinados momentos de tiempo han sido parcialmente abandonas a charrales, matorrales y bosques secundarios (ProDUS 2007; SINAC, 2007). Como consecuencia de un conjunto de elementos geológicos y geomorfológicos presentes en el área de estudio hacen que sean frecuentes los fenómenos sísmicos y, por lo tanto, muy vulnerable a producirse deslizamientos de tierra, especialmente en terrenos de pendiente pronunciada (Figura 2) que han sido deforestadas (Mende y Astorga, 2007).

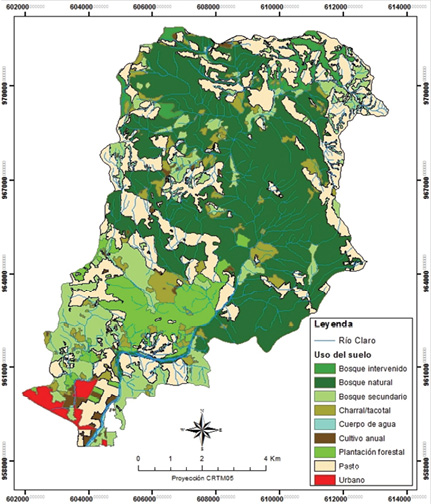
Figura 2. Mapa de pendientes (%)	Figura 3. Clasificación del uso del suelo

2.2. Distribución espacial de los procesos de erosión y sus factores condicionantes

Los procesos de erosión son el resultado de una interacción compleja entre factores naturales y factores antrópicos intrínsecamente determinados por las condiciones particulares del área de estudio. Dunne (1979) destacó de forma general la relevancia de los siguientes factores: clima, vegetación (uso del suelo), características del suelo y la topografía. Este autor, además, fue pionero en destacar el efecto de la deforestación y el cambio de uso del suelo en la erosión y sedimentación de cuencas tropicales.

Por lo tanto, debido a la confluencia conjunta de estos factores se supone que la distribución espacial de procesos de erosión no obedece a una relación aleatoria (Zinck et al., 2001; Huabin et al., 2005). Se realizó un inventario de los procesos de erosión observables en la imagen aérea de la misión CARTA (2005). Esta imagen aérea presenta el inconveniente de que aparecen áreas de sombra que se proyectan hacia el Oeste como consecuencia de la hora en que se tomó la imagen. Dichas áreas, especialmente visibles sobre las cavidades más profundas del terreno que forman los cauces hídricos, pueden ocultar procesos erosivos. El presente análisis espacial incorpora un porcentaje de incertidumbre estimado del ١٥ % en la asignación de las tipologías de erosión identificadas.

Con base en el mapa de inventario se realizó un análisis de autocorrelación espacial para aceptar o rechazar la hipótesis nula que establece que los valores de las entidades analizadas se distribuyen espacialmente de manera aleatoria con significancia estadística. En este caso, se trata de los procesos de erosión y sus valores son sus cuatro clases identificadas (laminar, surcos, cárcavas y deslizamientos). El análisis de autocorrelación calcula el índice de Moran, el p-valor y, un valor de Z que representa las desviaciones estándar, y cuyos datos informan en qué grado los valores (bajos y altos) tienden a agruparse mutuamente en el área de estudio.

Dado que el presente estudio es un análisis de susceptibilidad y no un análisis de amenazas, no se han incluido factores activadores como los de precipitaciones o fallas tectónicas. También se ha desestimado como factor condicionante el tipo de suelo, debido a que solamente se dispone de un único mapa en escala 1: 500 000 y, en el área de estudio, solo existen dos órdenes de suelos: inceptisoles y ultisoles.

En relación con las variables condicionantes se preseleccionó el siguiente grupo y se elaboraron las correspondientes capas de datos:

1. Uso del suelo. Este mapa fue elaborado mediante digitalización de polígonos sobre la imagen aérea de la misión CARTA (2005) a una escala 1: 5 000. El uso del suelo está dominado por bosque natural (41 %) junto con fragmentos extensos de bosque intervenido y secundario (17 %), pastizales predominantemente en la parte alta de la cuenca (25 %) y el resto (7 %) principalmente en plantaciones forestales de melina (Gmelina arborea) y de palma de aceite (Elaeis guianensis) (Figura 3).

2. Pendientes. Subdivididas en 10 clases representadas en porcentajes. Este mapa fue generado en una escala de 1: 5 000 a partir de un Modelo Digital de Elevación (MDE), el cual fue a su vez obtenido mediante una interpolación de contorno de curvas de nivel en intervalos de 10 metros (MINAE-CENIGA, 1998).

3. Subunidades geomorfológicas del terreno (TMS). Consiste en una clasificación del terreno a partir de datos geomorfológicos, edáficos y geológicos subdivididos en unidades homogéneas según las siguientes variables: 1) ángulo de pendiente, 2) relieve relativo, 3) dirección de pendiente y 4) densidad de drenaje. El mapa obtenido a partir de datos tomados en el campo correspondiente al área de estudio consta de 29 clases (Mende y Astorga, 2007).

4. Geología. Este mapa fue clasificado en 10 clases con base en datos geológicos tomados en el campo (Mende y Astorga, 2007).

5. Distancia a caminos. A partir de la digitalización de los caminos sobre la imagen CARTA (2005), se creó un área buffer de 100 metros alrededor de los caminos, a su vez subdividida en cuatro clases homogéneas de 25 metros cada una (Dai y Lee, 2002).

6. Distancia a los cauces hídricos. A partir de la digitalización de la red de drenaje sobre la imagen de CARTA (2005), se creó un área buffer de 100 metros alrededor de los caminos (Lee, 2005), a su vez subdividida en 4 clases homogéneas de 25 metros cada una.

2.3. Análisis estadístico bivariado de las ponderaciones de evidencia

El método de las ponderaciones de evidencia (Bonham-Carter, 1994) es una metodología de análisis estadístico bivariado que se basa en el cálculo de las probabilidades condicionales. Es el cálculo de la probabilidad de que ocurra un determinado evento, en este caso un proceso de erosión (E), habiéndose cumplido previamente otro, y dada la existencia de un determinado factor condicionante (B). Considerando todas las posibles combinaciones de presencia y ausencia de las dos variables en el modelo: B∩E, B̅∩E, B∩E̅, B̅∩E̅, la probabilidad condicionada de elegir un pixel con E, en una celda que contiene el factor B es:

(1)

Y las otras tres probabilidades condicionadas son:

	(2)
	(3)
	(4)

Aplicando el teorema de Bayes en los supuestos de presencia y ausencia del factor condicionante:

	(5)
	(6)

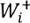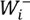Bonham-Carter et al. (1990) definió las ponderaciones de evidencia positivas y negativas ( y ) que combinan estas probabilidades condicionadas a partir de la definición de las odds ratio:

	(7)
	(8)
	(9)

Este método de las ponderaciones de evidencia se ha empleado considerando una variable explicativa de tipo binaria (presencia o ausencia de este factor). También se puede aplicar en el caso de variables con varias categorías y variables continuas transformadas en variables categóricas aplicando rangos. Los factores se expresaron en un número determinado de clases según el rango de valores en el área de estudio. El valor de las ponderaciones de evidencia calculado para cada clase de ese factor indica qué tan relevante es la presencia (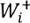) o la ausencia (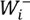) de esa clase para la ocurrencia de los procesos de erosión. De esta manera, si 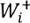es positivo significa que la presencia del factor es favorable para la ocurrencia de la erosión y viceversa si el valor resultante es negativo. Si 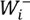es positivo significa que la ausencia de este factor es favorable para la ocurrencia de erosión y viceversa si es negativo. Por lo tanto, para cada factor existen cuatro posibles combinaciones, de las cuales se puede calcular la frecuencia, expresada como número de píxeles en las capas de datos tipo raster (Cuadro 1).

Cuadro 1. Cuatro posibles combinaciones correspondientes a un potencial factor condicionante de erosión y un mapa de inventario de fenómenos de erosión. Npi xi = número de pixeles

		B: Factor condicionante potencial de erosión
		Presente	Ausente
E: Erosión	Presente	Npi x1	Npi x2
	Ausente	Npi x3	Npi x4

A partir de las ecuaciones (8) y (9), las ponderaciones de evidencia pueden expresarse en número de pixeles de la siguiente forma:

	(10)
	(11)

Para el cálculo de las ecuaciones (10) y (11) todos los mapas en formato shapefile fueron convertidos en raster (1 150 columnas, 1 345 filas) con un tamaño de celda de 10 metros. Los mapas de los factores condicionantes basados en variables continuas se transformaron en variables categóricas aplicando rangos de clases. Todos los mapas se combinaron binariamente con el mapa de inventario de erosión y los valores de las ecuaciones se calcularon empleando la herramienta de análisis estadístico Zonal de ArcGIS 10.2. Como resultado de este proceso se descartaron para los análisis posteriores la variable geología, por mostrar una alta dependencia con la variable geomorfología y la variable distancia a carreteras por existir una única ruta vial para vehículos y, por lo tanto presentar valores no significativos.

2.4. Análisis multivariado de regresión logística binaria

La regresión logística es un tipo de análisis de regresión utilizado para predecir el resultado de una variable categórica (una variable que puede adoptar un número limitado de categorías) en función de un conjunto predeterminado de variables independientes. En la presente investigación se aplica un modelo de regresión logística binaria, es decir, la variable categórica es dicotómica, puede adquirir dos valores (presencia o ausencia de un evento de erosión).

Para poder plantear una función lineal, es necesario realizar una trasformación logarítmica (logit). Aplicando esta función al caso de estudio:

(12)

Los coeficientes en una regresión logística binaria se estiman mediante el sistema de máxima verosimilitud. El valor exponencial de cada uno de los coeficientes estimados (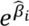) es el odds ratio de la probabilidad de ocurrencia de erosión frente a la probabilidad de no erosión en términos marginales de variación de una unidad en la variable explicativa. Siendo P{E} la probabilidad de ocurrencia de un fenómeno de erosión y siendo n el número de variables hipotéticas explicativas condicionantes o predictoras.

A partir de esta función es posible calcular la probabilidad de ocurrencia de erosión, de la siguiente forma:

(13)

Para el planteamiento de la ecuación de regresión logística binaria, el primer paso consistió en relacionar cada uno de los polígonos de erosión con una coordenada determinada de forma aleatoria, dentro de los límites del polígono. A este conjunto de puntos en formato archivo de datos se le asocia una tabla de atributos con los valores cuantitativos y categóricos de las variables condicionantes. En total se obtuvieron 347 puntos observables de eventos de erosión. El segundo paso consistió en distribuir puntos aleatorios dentro de los límites del área de estudio, para ello se delimitó previamente un área buffer mínima de 50 metros alrededor de los puntos de erosión para evitar cualquier coincidencia espacial (Dai y Lee, 2005). Este proceso se llevó a cabo mediante la herramienta Create Random Points de ArcGIS 10.2. De esta forma se obtuvieron 330 puntos sin evidencia de erosión. Similarmente, se le asoció una tabla de atributos con los valores de todos los factores.

Las bases de datos de los puntos con y sin erosión se integraron en una sola base para realizar la regresión logística binomial mediante el programa estadístico SPSS v21 (SPSS Inc., Chicago, IL., EE. UU.). Los puntos de erosión se calificaron como uno (1) y los puntos de no erosión se calificaron como cero (0).

Para la selección de las variables explicativas incorporadas en la ecuación de regresión final se procedió a jerarquizar los valores de las ponderaciones de evidencia totales calculadas en el procedimiento anterior y, de esta manera, descartar los factores que resultaron menos relevantes. Para ello se evaluó el comportamiento de cada una de las variables independientes con la dependiente mediante un análisis bivariado, como primer sustento estadístico para priorizar la incorporación de las variables en el modelo y el orden de estas, esperando que se encuentren en la regresión final las que mejor expliquen la probabilidad de ocurrencia de erosión. El análisis bivariado consiste en un contraste de dependencia 𝜒². Mediante este procedimiento se seleccionaron las variables estadísticamente relevantes con las cuales se formula la ecuación de regresión definitiva.

Una vez planteado el modelo final de regresión logística es necesario realizar un conjunto de ajustes en las variables independientes del modelo debido a su diferente naturaleza de mediación. Se introducen variables cuantitativas con diferente unidad de medida y variables categóricas compuestas por un amplio conjunto de clases. La solución al primer inconveniente consiste en normalizar todos los valores en una unidad de medición común (Nefeslioglu et al., 2008). La solución tradicional al segundo problema es crear variables binarias o dicotómicas (dummy) para cada una de las diferentes clases (Guzzetti et al., 1999; Dai y Lee, 2002). Si el número de parámetros es bajo, esta propuesta podría ser conveniente; sin embargo, si existen muchos parámetros, como en el presente estudio, la función lineal resultante sería muy larga, su cálculo muy complejo y la evaluación estadística de los resultados de la regresión final para cada variable independiente puede presentar errores de interpretación y multicolinealidad (Ayalew y Yamagishi, 2005).

Por estas razones, en el presente estudio se ha optado por un enfoque basado en la normalización de los valores de todas las clases en una misma escala mediante su odds ratio correspondiente a su peso de evidencia positivo (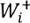) calculado anteriormente en el análisis bivariado e incorporados en la base de datos del SIG.

2.5. Análisis multivariado de probabilidad condicional conjunta

A diferencia del modelo de regresión logística binaria, el planteamiento teórico del modelo de probabilidad condicional consiste en predecir la probabilidad futura de que en un determinado pixel (p), perteneciente al área de estudio, suceda un evento de erosión de determinada tipología condicionado a la presencia previa y simultánea de un conjunto de valores correspondientes a los factores explicativos considerados. Es decir, el pixel p incorpora un número m de valores, v1(p), v2(p), ... vm(p), uno para cada factor o capa de datos (Chung y Fabbri, 1999).

Partiendo de la proposición anterior expresada de la siguiente forma:

Fp: “El pixel p será afectado en el futuro por un proceso de erosión de una tipología determinada”

El planteamiento teórico del cálculo de la probabilidad condicional conjunta será el siguiente:

(14)

Dado que Fp expresa las áreas (pixeles) desconocidas que serán afectadas por futuros procesos de erosión, para estimar la probabilidad condicional conjunta se utilizarán los datos de los procesos de erosión pasados ocurridos hasta la fecha de su recolección. De esta forma se define:

Ep: “El pixel p ha sido afectado en el pasado por un proceso de erosión de una tipología determinada”.

Por lo tanto, la probabilidad condicional conjunta de que el pixel p haya sido afectado por un determinado proceso de erosión ocurrido en el pasado sujeto a la condición de que p incorpora los valores de v1(p), v2(p), ... vm(p) es igual a:

(15)

El cálculo de esta probabilidad es complejo en términos operativos debido a la circunstancia de que las variables explicativas son categóricas y, por lo tanto, para salvar esta dificultad, se ha decidido usar el teorema de Bayes, adaptado a la ecuación de las ponderaciones de evidencia positivas (Soares-Filho et al., 2010; Mas y Flamenco, 2011).

La ventaja de este método sobre el de regresión logística es el hecho de no estar sujeto a los supuestos de los métodos paramétricos que, en general, los datos espaciales suelen violar (Haggett et al., 1977). Sin embargo, el método de Bayes debe cumplir el supuesto estadístico de presentar independencia condicional entre los patrones espaciales (v1(p), v2(p), ... vm(p)). Este supuesto puede comprobarse mediante pruebas por parejas como el coeficiente V de Cramer (Bonham-Carter, 1994). Este coeficiente varía entre cero y uno, cero indicando variables totalmente independientes y uno totalmente correlacionadas.

El cálculo de la probabilidad condicional conjunta mediante el teorema de Bayes se muestra de la siguiente forma:

(16)

Esta ecuación se puede expresar en términos de odds, que se definen como la razón entre la probabilidad de que un evento ocurra y la probabilidad de que no ocurra de la siguiente manera:

(17)

Donde 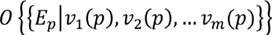es el odds condicional de la ocurrencia de un evento de erosión dada la presencia de un conjunto de patrones espaciales y 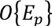es el odds de la ocurrencia previa de un evento de erosión. El cociente entre las dos probabilidades restantes de la ecuación se conoce con el término de “ratio razón suficiente”, cuyo logaritmo natural es precisamente el peso de evidencia positivo (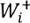) según la ecuación (7).

De esta forma la probabilidad condicional conjunta puede expresarse en los términos siguientes:

(18)

Donde 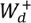es el peso de evidencia positivo de la ocurrencia previa de los procesos de erosión, es decir, de :

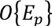(19)

2.6. Validación de los resultados

En el presente estudio se han utilizado dos métodos para validar teóricamente la calidad predictiva de los mapas de susceptibilidad. En primer lugar, el método del ratio de acierto (success rate), que calcula el porcentaje acumulado de todos los procesos de erosión observables que ocurren en los rangos de susceptibilidad más altos (Chung y Fabbri, 1999; Van Westen et al., 2003; Lee, 2005). El procedimiento consiste en reclasificar primeramente el mapa de susceptibilidad en diez clases homogéneas cuyos valores son ordenados inversamente de mayor a menor y a continuación se cuenta el número de pixeles de erosión contenidos en cada uno de los rangos (deciles).

El segundo procedimiento se basa en el cálculo de la curva ROC (siglas en inglés de Receiver Operating Characteristic o Característica Operativa del Receptor) (Pontius y Schneider, 2001) y el Área debajo de la Curva o AUC (siglas en inglés de Area Under the Curve) (Zweig y Campbell, 1993). La curva ROC calcula la proporción de los puntos de ocurrencia de un evento de erosión pronosticados de forma correcta (sensibilidad) contra la proporción de puntos de no ocurrencia de erosión pronosticados erróneamente (1-especificidad) para todas las posibles combinaciones de umbrales de discriminación entre ambos resultados.

3. Resultados

3.1. Distribución espacial y tipología de los procesos de erosión

El mapa de inventario de los procesos de erosión observables en la cuenca del río Claro correspondiente al año 2005 diferenciando su clasificación tipológica se muestra en la Figura 4.

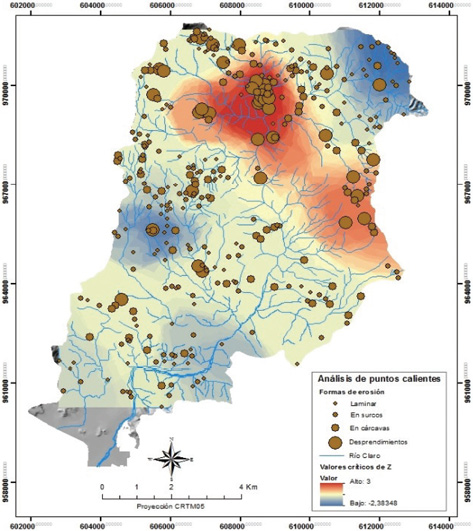
Figura 4. Análisis de puntos calientes (hot spot analysis) de la distribución espacial de las clases de procesos de erosión correspondientes al año 2005

Los resultados del análisis de autocorrelación mediante el índice de Moran, se muestran en el Cuadro 2 y en la Figura 5. Según estos datos se rechaza la hipótesis nula y se acepta la hipótesis alternativa con significancia estadística del 95 % de que existe un alto grado de agregación espacial y específicamente entre los valores altos, es decir, los deslizamientos.

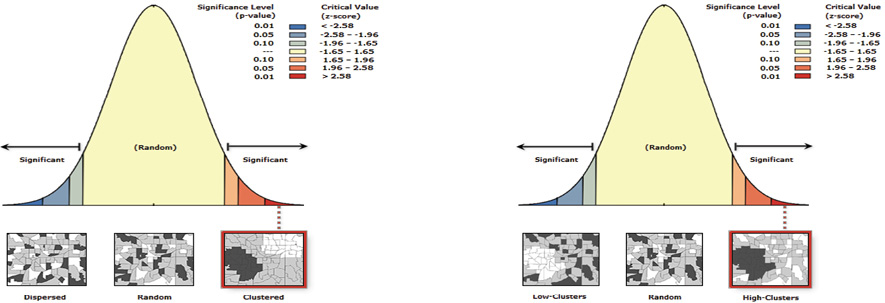
Figura 5. Informes de los resultados del análisis de autocorrelación espacial (Índice de Moran) y de Valores altos y bajos mediante las herramientas de Análisis Estadístico Espacial de un SIG de la distribución espacial de los procesos de erosión

Cuadro 2. Resultados del análisis de autocorrelación (Índice de Moran)

Resultados del análisis de autocorrelación espacial	Autocorrelación espacial (Índice de Moran)	Valores altos y bajos
Índice	0,222300	0,000116
Z score	9,157857	3,962526
Valor de p	0,000000	0,000074

Con base en estos resultados, se realizó un análisis de puntos calientes (hot spot analysis) posteriormente interpolados mediante el método kriging, obteniéndose una imagen tipo raster (Figura 4) en la cual se destacan en color rojo las áreas donde se agrupan los valores de erosión más altos (cárcavas y deslizamientos) y en color azul los valores más bajos (laminar y surcos).

3.2. Análisis estadístico bivariado de las ponderaciones de evidencia

Los resultados de las ponderaciones de evidencia (Cuadro 3) muestran que las clases que presentan un valor positivo más alto, son las pertenecientes al factor uso del suelo, concretamente las clases pasto y cultivo anual. El resto presentó valores negativos relativamente altos, lo cual evidencia que su presencia no es significativa para la ocurrencia de erosión. En relación con las subunidades geomorfológicas del terreno, se destacan valores positivos relevantes en los escarpes tectónicos y acantilados en la cresta, localizados en terrenos de pendiente alta a pronunciada y moderada.

Los cálculos obtenidos en las diferentes clases de pendiente no presentan valores muy altos, ni los positivos ni los negativos, y, como consecuencia, no son, en principio, buenos predictores en esta área de estudio. A pesar de estos resultados, se ha decidido mantener este factor como relevante para los análisis posteriores porque, en primer lugar, se comprueba que los valores de las ponderaciones de evidencia positivas más altos se concentran en las clases de pendientes de un rango entre el 30 % y un 60 % localizadas en la parte alta de la cuenca, y, en segundo lugar, la ausencia de este factor reduce la validez de los análisis estadísticos posteriores. Además, es un factor que incorpora un efecto interno de riesgo de amenazas por deslizamientos y es un elemento importante para la zonificación de áreas críticas.

Cuadro 3. Resultados de las ponderaciones de evidencia positivas según los factores condicionantes y sus respectivas clases

Mapa	Clase	Ponderaciones de evidencia positivos
Uso del suelo	Cultivo anual	1,108307
	Cultivo permanente	-2,027335
	Pasto	1,215835
	Charral/tacotal	0,069965
	Bosque secundario	-1,245579
	Bosque intervenido	-0,660981
	Bosque natural	-2,086627
Geomorfología	Cuaternario-DA. Predominancia de arenas	-3,534156
	Cuaternario-DA. Predominancia de limos/arcillas	0
	Cuaternario-DA. Terrazas fluviales	-3,675968
	Cuaternario-Depósitos de cauces fluviales recientes	-2,444963
	Escarpes tectónicos. FB – UC. Relieve alto a pronunciado	-1,036052
	Escarpes tectónicos. FB – UC. Relieve moderado	1,410016
	Escarpes tectónicos, FT – UZ. Relieve alto a pronunciado	-0,055048
	Acantilados en la cresta. FT – UZ. Relieve alto a pronunciado	0,760861
	Acantilados en la cresta. FT – UZ. Relieve moderado	0,453376
	Acantilados en la cresta. FT – UL. Relieve alto a pronunciado	0,382464
	Zona alta del talud SW. FT – UZ. Relieve alto a pronunciado	-0,055048
	Zona alta del talud SW. FT – UZ. Relieve moderado	-0,899323
	Zona alta del talud SW. FT – UZ. Relieve bajo	0,914147
	Depósitos recientes de deslizamientos. Relieve alto a pronunciado	0,408933
	Depósitos recientes de deslizamientos. Relieve moderado	-0,398021
	Depósitos recientes de deslizamientos. Relieve bajo	0,474368
	Altiplanos dentro del talud SW. FB – UCn. Relieve alto	-0,584225
	Altiplanos dentro del talud SW. FB – UCn. Relieve moderado.	-0,710031
	Altiplanos dentro del talud SW. FT – UZ. Relieve moderado	-0,491253
	Altiplanos dentro del talud SW. FT – UL. Relieve moderado	-0,625179
	Zona baja del talud SW. FB – Ucl. . Relieve alto a pronunciado	-0,625179
	Zona baja del talud SW. FB – Ucl. Relieve moderado	-0,303144
	Zona baja del talud SW. FB – Ucl. Relieve bajo	0,261137
	Zona baja del talud SW. FT – UZ. Relieve alto a pronunciado	-0,678456
	Zona baja del talud SW. FT – UZ. Relieve moderado	-0,592491
	Zona baja del talud SW. FT – UZ. Relieve bajo	0
	Zona baja del talud SW. FCu. Relieve moderado	0,655684
	Zona baja del talud SW. FCu. Relieve bajo	0
	Depósitos recientes de deslizamientos. Relieve bajo	-1,547558
Pendiente (%)	0-15 %	-0,700171
	15-30 %	0,161601
	30-45 %	0,323244
	45-60 %	0,251546
	60-75 %	0,144381
	75-90 %	-0,194110
	90-105 %	-1,107942
	105-120 %	-1,198524
	120-135 %	-0,749197
	135%-150 %	-1,308434
Distancia a cauces	< 25 m del cauce	-0,263981
	25-50 m del cauce	0,017434
	50-75 m del cauce	0,009201
	75-100 m del cauce	-0,013668

DA: Depósitos aluviales, FB: Formación Brito, FT: Formación Térraba, UCn: Unidad Cajón, UZ: Unidad Zapote, UL: Unidad Lagarto. UCl: Unidad Cañablancal, FCu: Formación Curré.

3.3. Análisis multivariado de regresión logística binaria

Los resultados del análisis de regresión logística binaria se resumen en los siguientes coeficientes y sus estadísticos correspondientes resumidos en los Cuadros 4 y 5.

Cuadro 4. Variables incluidas en el modelo multivariado de regresión logística

	B	E.T	Wald	gl	Sig.	Exp (B)	I.C. 95 % para Exp (B)
							Inferior	Superior
Geomorfología	0,343	0,103	11,031	1	0,001	1,409	1,151	1,725
Uso	0,657	0,064	106,743	1	0,000	1,930	1,704	2,186
Pendiente	1,050	0,279	14,129	1	0,000	2,859	1,653	4,943
Distancia a cauces	0,448	0,189	5,629	1	0,018	1,564	1,081	2,264
Constante	-2,810	0,381	54,491	1	0,000	0,060

Cuadro 5. Resumen de estadísticos del modelo de regresión logística

Estadístico	Valor
-2 log de la verosimilitud	782,161
R cuadrado de Nagelkerke	0,274
Chi cuadrado	11,168
Gl.	8
Sig.	0,449
Porcentaje global pronosticado	70,6

Los resultados generales son moderadamente positivos y se puede afirmar que la ecuación de regresión obtenida es capaz de predecir la probabilidad de ocurrencia de un proceso de erosión por encima del 70 % y, como consecuencia, las variables explicativas independientes incluidas en el modelo aportan significativamente a la predicción de la variable dependiente. El valor de R cuadrado de Nagelkerke indica que el modelo propuesto explica el 27,4 % de la varianza de la variable dependiente.

A efectos de comparar los resultados de la regresión obtenidos, se construyó, un modelo alternativo formado por las mismas variables independientes en su formato original, es decir, la variable pendiente como cuantitativa y el resto de variables como categóricas. Los resultados de la ecuación de regresión resultante mostraron niveles de predicción de la variable independiente, ligeramente superiores (por ejemplo, un porcentaje global explicado del 75,2 %). Sin embargo, se descartó su inclusión debido a su complejidad operativa.

Cuadro 6. Clasificación de niveles de susceptibilidad y su porcentaje de cobertura mediante el modelo de regresión logística binaria

Rango de probabilidad	Clasificación	Área (%)
0,09021– 0,2375	Muy baja	23,5928
0,2375 – 0,3717	Baja	33,2746
0,3717 – 0,5224	Moderada	15,7816
0,5224 – 0,6959	Alta	7,7409
0,6959 – 0,9251	Muy alta	16,2213

Finalmente, la ecuación de regresión logística se aplicó a todo el área de estudio por medio de ArcGIS 10.2, se calculó la susceptibilidad (P{E}) mediante la ecuación (13) para cada pixel de tamaño 10 metros y el mapa resultante (Figura 6), fue reclasificado en cinco niveles mediante el sistema de Natural Breaks que se consideró como el más apropiado para el presente caso porque el sistema no permitió dividir el mapa en cinco categorías y además la diferencia en el rango de valores de la categoría superior no es muy significativa.

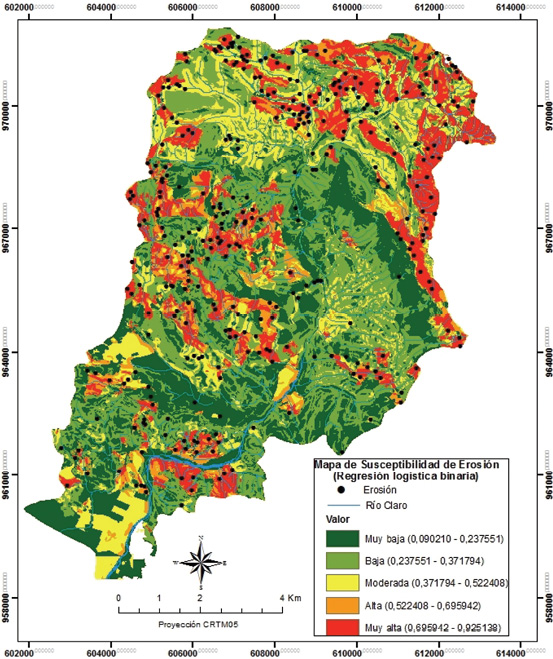
Figura 6. Mapa de susceptibilidad de erosión según el método de regresión logística binaria e inventario de puntos de erosión

3.4. Análisis multivariado de probabilidad condicional conjunta

Siguiendo el procedimiento para el cálculo de la probabilidad condicional conjunta mediante la ecuación (18) y considerando las cuatro capas de datos o patrones espaciales seleccionadas previamente y aceptando el supuesto de independencia condicional entre las variables explicativas, se aplicó a toda el área de estudio por medio de ArcGIS 10.2 y el mapa de susceptibilidad resultante se muestra en la Figura 6. Al igual que el modelo de regresión binaria, el mapa de susceptibilidad obtenido fue reclasificado en cinco niveles mediante el sistema de desviación estándar que se consideró también como el más apropiado dada la alta dispersión en la distribución de los datos.

Cuadro 7. Clasificación de niveles de susceptibilidad y su porcentaje de cobertura mediante el modelo de probabilidad condicional conjunta

Rango de probabilidad	Clasificación	Área (%)
0,000044 – 0,018025	Muy baja	37,88 %
0,018025 – 0,058892	Baja	44,67 %
0,058892 – 0,142262	Moderada	7,30 %
0,142262 – 0,246882	Alta	5,44 %
0,246882 – 0,416890	Muy alta	4,68 %

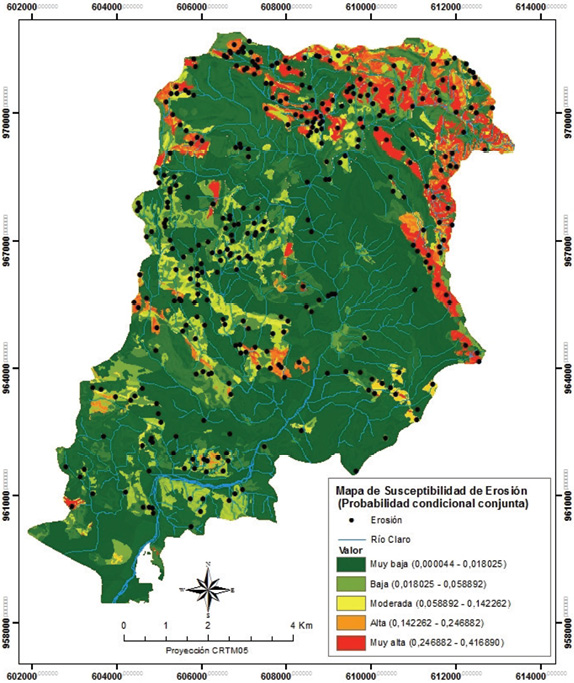
Figura. 7. Mapa de susceptibilidad de erosión según el método de probabilidad condicional conjunta correspondiente al año 2005

3.5. Validación de los modelos

El método del ratio de acierto se aplicó sobre los dos mapas de susceptibilidad obtenidos mediante los métodos de regresión logística binaria y de probabilidad condicional conjunta (Figuras 6 y 7) cuyo resultado se muestra en la Figura 8. Como puede apreciarse, ambos métodos presentan curvas con niveles de precisión o predictibilidad altos, siendo más alto el correspondiente al método de probabilidad condicional conjunta.

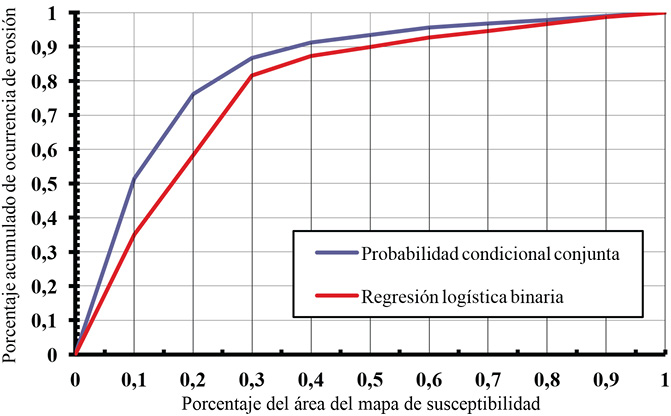
Figura 8. Curvas del ratio de acierto (success rate) de los mapas de susceptibilidad de erosión calculados mediante los métodos de regresión logística y probabilidad condicional conjunta

El método de probabilidad condicional conjunta presenta una curva ROC de mayor área que la que presenta el método de regresión logística binaria (Figura 9) y, por lo tanto, su AUC es también superior (Cuadros 6 y 7), como consecuencia se concluye que el primero presenta un grado de predicción ligeramente superior al segundo.

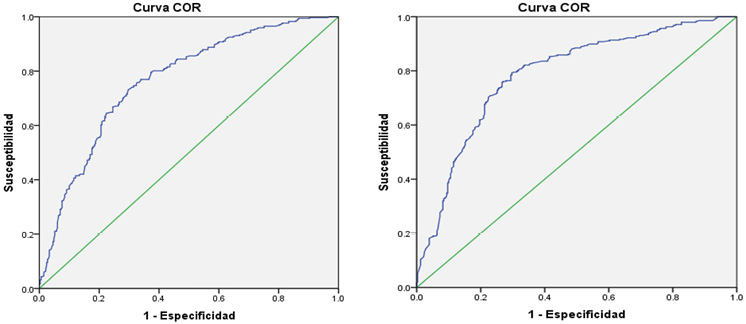
Figura 9. a) Izquierda: la curva ROC del mapa de susceptibilidad de erosión correspondiente al método de regresión logística binaria y b) Derecha: la curva ROC del mapa de susceptibilidad de erosión basado en el método de probabilidad condicional conjunta

Cuadro 6. Área bajo la curva (AUC) del método de regresión logística binaria

Área	Error típico	Sig. Asintótica	Intervalo de confianza asintótico al 95 %
			Límite inferior	Límite superior
0,765	0,018	0,000	0,730	0,801

Cuadro 7. Área bajo la curva (AUC) del método de probabilidad condicional conjunta

Área	Error típico	Sig. Asintótica	Intervalo de confianza asintótico al 95 %
			Límite inferior	Límite superior
0,786	0,018	0,000	0,751	0,821

4. Discusión

Los resultados del análisis estadístico bivariado basado en el cálculo de las ponderaciones evidencia positivas, muestran la relevancia dominante del factor de uso y cobertura del suelo sobre los demás factores condicionantes. A diferencia del estudio de Van Westen et al. (2003) sobre susceptibilidad de deslizamientos, en el que destaca la importancia del factor geomorfológico detallado para lograr un mapa de susceptibilidad con mayor capacidad de predicción. El presente estudio también incorpora en su modelo una capa de datos geomorfológicos muy precisa, caracterizada como subunidades geomorfológicas del terreno (TMS) (Mende y Astorga, 2007) que en una clase específica de escarpes tectónicos de relieve moderado presenta una muy alta ponderación de evidencia positiva = 1,41) superior incluso a la clase de pasto en el factor uso del suelo = 1,2158) y, además, elevó notablemente el grado de precisión de los mapas de susceptibilidad.

Los valores de los coeficientes obtenidos en el modelo de regresión logística binaria normalizada (Cuadro 4) indican que todos los factores están positivamente correlacionados con la probabilidad de ocurrencia de procesos de erosión, son significativos en el modelo (p<0,05) y la mayor importancia relativa corresponde al factor uso del suelo, superior al factor geomorfológico. Estos resultados difieren de otros estudios que utilizaron la misma metodología. Para Ayalew y Yamagishi (2004) el parámetro más relevante en su modelo es la distancia a las carreteras; para Lee (2005) es la pendiente; para Pineda et al. (2011) es la morfología de pendientes o tipo de relieve; para Akbari et al. (2014) es la pendiente seguida de la distancia a carreteras; para Lee et al. (2016) es la pendiente seguida del drenaje del suelo. A diferencia de los estudios anteriores que se focalizan en inventariar exclusivamente los deslizamientos, el presente trabajo incluye todas las posibles formas de erosión y, como consecuencia, los factores intrínsecos del terreno poseen una influencia relativa más baja.

El método de validación del mapa de susceptibilidad de la regresión logística obtenido mediante el cálculo del área bajo la curva en la gráfica del ratio de acierto, el cual evalúa cualitativamente el grado de precisión predictiva, es del 78,47 %. Comparativamente en el estudio de Dai y Lee (2002) es del 85 %, en Lee (2005) ese mismo cálculo es del 78,6 % y del 80,01 % en Lee et al. (2016). Aplicando el método de validación ROC, este es del 76,5 %, siendo en el estudio de Ayalew y Yamagishi, (2004) de un 83,58 %.

En el modelo de probabilidad condicional conjunta, el Área Bajo la Curva (ABC) de la gráfica del ratio de acierto es del (83,81 %) y el ABC en el análisis de ROC es del 78,6 %. En conclusión, el método de probabilidad condicional conjunta mediante el teorema de Bayes y el cálculo de las ponderaciones de evidencia positivas presenta un mayor grado de predicción que el de regresión logística binaria, además de un conjunto de ventajas operativas.

5. Conclusiones

El propósito del presente estudio fue evaluar cuantitativamente el estado de conservación de una cuenca hidrográfica en el trópico húmedo de Costa Rica en términos de susceptibilidad de erosión. El método de probabilidad condicional conjunta además de poseer un nivel de precisión predictiva ligeramente superior al método de regresión logística binaria, posibilita un mayor grado de detalle para clasificar el nivel de muy alta susceptibilidad. La validez de cualquiera de estos métodos depende de la disponibilidad de los datos correspondientes a las variables explicativas en el área de estudio, las cuales deben ser normalizadas para lograr la validez estadística de los modelos.

En general, estas áreas se caracterizan por un uso del suelo de pastos degradados, una ganadería extensiva en terrenos de alta a moderada pendiente (30 % - 60 %) y una geomorfología de escarpes tectónicos de relieve moderado. Como consecuencia de estos resultados, se llega a la conclusión de que determinados sitios de la cuenca soportan una elevada degradación del terreno y una muy alta probabilidad de erosión y vulnerabilidad biofísica. Por este motivo se recomienda implementar, preferentemente, proyectos de reforestación con especies nativas complementados con prácticas de manejo de la actividad pecuaria más sostenibles, que permitan la restauración ecológica integral del ecosistema y una provisión integral de servicios ecosistémicos.

6. Agradecimientos

Agradezco de manera especial a mi familia por el apoyo incondicional a lo largo de esta investigación, a la Maestría en Manejo de Recursos Naturales (UNED), a mis profesores y a todas aquellas personas que de manera desinteresada comparten sus investigaciones y su conocimiento en la red. Agradecemos también a la revista y a las personas revisoras anónimas por sus oportunos comentarios que ayudaron a mejor la versión final del artículo.

7. Referencias

Akbari, A., Yahaya, F. B. M., Azamirad, M., & Fanodi, M. (2014). Landslide Susceptibility Mapping Using Logistic Regression Analysis and GIS Tools. Electronic Journal of Geotechnical Engineering, (14), 1687-1696.

Arce, R. (2004). Resumen diagnóstico cuenca Reventazón. Consultoría para Proyecto de Redes Comunitarias para la Gestión del Riesgo. San José. Costa Rica.

Ayalew, L., & Yamagishi, H. (2004). The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology, 65(1-2), 15-31. doi: 10.1016/j.geomorph.2004.06.010

Bayard, B.; Curtis, M. J., & Shannon, D. (2006). The Adoption and Management of Soil Conservation Practices in Haiti: The Case of Rock Walls. Agricultural Economics Review, (2), 28-39.

Bonham-Carter, G. F. (1994). Geographic Information Systems for Geoscientists: Modelling with GIS, Comp. Meth. Geos., (Vol. 13), Pergamon Press.

Bosch, J. M., & Hewlett, J. D. (1982). A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. Journal of Hydrology 55(1-4), 3-23. doi: 10.1016/0022-1694(82)90117-2

Bruijnzeel, L. A. (2004). Hydrological functions of tropical forests: not seeing the soil for the trees? Agriculture, Ecosystems and the Environment, (104), 185-228. Recuperado de http://www.elsevier.com/locate/agee

Calder, I. R. (2002). Forests and hydrological services: reconciling public and science perceptions. Land Use and Water Resources Research, (2), 2.1-2.12. Recuperado de https://ageconsearch.umn.edu/ bitstream/47860/2/paper02-02.pdf

Carrara, A., Cardinali, M., Detti, R., Guzzetti, F., Pasqui, V., & Reichenbach, P. (1991). GIS techniques and statistical models in evaluating landslide hazard. Earth Surface Processes and Landforms 16(5), 427-445. doi: 10.1002/esp.3290160505

Castellanos Abella, E. A., & Van Westen, C. J. (2007). Generation of a landslide risk index map for Cuba using spatial multi-criteria evaluation. Journal of the International Consortium on Landslides, 4(4), 311-325. doi: 10.1007/s10346-007-0087-y

Chomitz, K. M., & Kumari, K. (1996). The domestic benefits of tropical forests: A critical review emphasizing hydrologic functions. World Bank Policy Research Working Paper, N.° 1601. Retrieved from http://documents.worldbank.org/curated/en /212631468765869841/pdf/multi-page.pdf

Chung, C. J., Fabbri, A., & Van Westen, C. J. (1995). Multivariate regression analysis for landslide hazard zonation. In: A. Carrara and F. Guzetti (Eds.), Geographical Information Systems in Assessing Natural Hazards (Vol. 5), 107-103. Kluwer. doi: 10.1007/978-94-015-8404-3_7

Chung, C. J., & Fabbri, A. G. (1999). Probabilistic prediction models for landslide hazard mapping. Photogrammetric Engineering & Remote Sensing 65(12), 1389-1399. Retrieved from https://pdfs.semanticscholar.org/60d7/ 521e8a30440b9c95046a5e451ebae8cde9af.pdf

Dai, F. C., & Lee, C. F. (2002). Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 42(3-4), 213-228. doi: 10.1016/S0169-555X(01)00087-3

Douglas, I. (1996). The impacts of land-use changes, especially logging, shifting cultivation, mining and urbanization on sediment yields in humid tropical Southeast Asia: a review with special reference to Borneo. International Association of Hydrological Science (IAHS), (236), 463-471. Retrieved from https://www.researchgate.net /publication/237552926

Dunne, T. (1979). Sediment yield and land use in tropical catchments. Journal of Hydrology, 42(3-4), 281-300. doi: 10.1016/0022-1694(79)90052-0

Falkenmark, M., & Chapman, T. (Eds.). (1989). Comparative hydrology. An ecological approach to land and water resources. Paris: UNESCO.

FAO [Organización de las Naciones Unidas para la Agricultura y la Alimentación]. (1984). Directrices sobre la Planificación del Aprovechamiento de la Tierra. Roma: Colección FAO: Desarrollo, N.º 1.

Fritsch, J. M. (1993). The hydrological effects of clearing tropical rain forest and the implementation of alternative land users. International Association of Hydrological Science (IAHS), (216), 53-66. Retrieved from https://iahs.info/uploads/dms/iahs_216_0053.pdf

Gilmour, D. A. (1977). Effect of rainforest logging and clearing on water yield and quality in a high rainfall zone of north-east Queensland. In E.M. O’ Loughlin & L. J. Bren (Eds.), Proceedings of the first National Symposium of forest Hydrology. Melbourne: Institution of Engineers Australia, 156-160.

Guzzetti, F., Carrara, A., Cardinali, M., & Reichenbach, P. (1999). Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology, 31(1-4), 181-216. doi: 10.1016/S0169-555X(99)00078-1

Haggett, P., Cliff, A. D., & Frey, A. (1977). Locational Analysis in Human Geography. New York: Wiley & Sons.

Herrera, W. (1986). Clima de Costa Rica. (Vol. 2). En L. D. Gómez (Ed.), Vegetación y Clima de Costa Rica. San José: EUNED.

Huabin, W., Gangjun, L., Weiya, X., & Gonghui, W. (2005). GIS-based landslide hazard assessment: an overview. Progress in Physical Geography, 29(4), 548-567. doi: 10.1191/0309133305pp462ra

Kaimowitz, D. (1996). Livestock and Deforestation: Central America in the 1980s and 1990s: A Policy Perspective. Jakarta: Centre for International Forestry Research. Retrieved from http://www.cifor.org/publications/pdf_files /SPubs/SP-LStock-n.pdf

Kiersch, B. (2000). Land use impacts on water resources: A literature review. Land-Water Linkages in Rural Watersheds. Electronic Workshop [Discussion Paper N.º 1]. Rome: FAO. Retrieved from http://www.mekonginfo.org/assets/midocs/ 0001419-inland-waters-land-use-impacts-on-water-resources-a-literature-review.pdf

Lee, S. (2005). Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. International Journal of Remote Sensing, 26(7), 1477-1491. doi: 10.1080/01431160412331331012

Lee S.; Jeon, S. W.; Oh, K. Y., & Lee, M. J. (2016). The spatial prediction of landslide susceptibility applying artificial neural network and logistic regression models: A case study of Inje, Korea. Open Geosciences, 8(1), 117-132. doi: 10.1515/geo-2016-0010

Lobo, J. y Bolaños, F. (Eds.). (2005). Historia Natural de Golfito, Costa Rica. Santo Domingo: INBio.

Mas, J. F. y Flamenco-Sandoval, A. (2011). Modelación de los cambios de coberturas/uso del suelo en una región tropical de México. GeoTrópico, 5(1), 1-24. Recuperado de http://www.geotropico.org/NS_5_1_Mas-Flamenco.pdf

Mende, A., & Astorga, A. (2007). Incorporating geology and geomorphology in land management decisions in developing countries: A case study in Southern Costa Rica. Geomorphology, 87(1-2), 68-89. doi: 10.1016/j.geomorph.2006.06.043

MINAE-CENIGA. (1998). Información Cartográfica de la Misión TERRA-Costa Rica. Ministerio de Ambiente, Energía y Minas.

Nefeslioglu, H. A., Gokceoglu, C., & Sonmez, H. (2008). An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Engineering Geology, 97(3-4), 171-191. doi: 10.1016/j.enggeo.2008.01.004

Pérez, S., Alvarado, A. y Ramírez, E. (1978). Manual Descriptivo del Mapa de Asociaciones de Subgrupos de Suelo de Costa Rica. Escala 1:200.000. Oficina de Planificación Sectorial Agropecuario. IGN-MAG-FAO. San José.

Pineda, M. C., Elizalde, G., Viloria, J. (2011). Determinación de áreas susceptibles a deslizamientos en un sector de la cordillera de la costa central de Venezuela. Interciencia, 36(5), 370-377. Recuperado de http://www.redalyc.org/pdf/339/33918012008.pdf

Pontius, R. G., & Schenider, L. (2001). Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agriculture, Ecosystems and Environment, 85(1-3), 239-248. doi: 10.1016/S0167-8809(01)00187-6

Pourghasemi, H. R., Pradhan, B., Gokceoglu, C., & Moezzi, D. (2012). Landslide Susceptibility Mapping Using a Spatial Multi Criteria Evaluation Model. In B. Pradhan, & M. Buchroithner (Eds.). Terrigenous Mass Movements. Berlin:Springer-Verlag.

Pradhan, B. (2010). Application of an advanced fuzzy logic model for landslide susceptibility analysis. International Journal of Computational Intelligence Systems, 3(3), 370-381. doi: 10.2991/ijcis.2010.3.3.12

Pradhan, B., & Lee, S. (2010). Regional landslide susceptibility analysis using backpropagation neural network model at Cameron Highland, Malaysia. Landslides, 7(1), 13-30. doi: 10.1007/s10346-009-0183-2

ProDUS. (2007). Diagnóstico. Plan regulador cantonal de Golfito (Tomo I). San José: Universidad de Costa Rica.

Purwanto, E. (1999). Erosion sediment delivery and soil conservation in an upland agricultural catchment in West Java, Indonesia. (PhD. Thesis). Vrije Universiteit, Amsterdam.

Riba, L. (2007). Diagnóstico socio ambiental de la región Sur de Costa Rica. San José: Universidad de Costa Rica.

Rijsdijk, A., & Bruijnzeel, L. A. (1991). Erosion sediment yield and land use patterns in the upper Konto watershed. East Java, Indonesia (Vol. 18). Indonesia: Konto River Project Communication.

Shahabi, H., & Hashim, M. (2015). Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Scientific Reports, 5, 1-15. doi: 10.1038/srep09899

SINAC [Sistema Nacional de Áreas de Conservación]. (2007). Análisis de vacíos de conservación en Costa Rica (Vol. 1) San José: Asociación Conservación de la Naturaleza. Recuperado de http://cro.ots.ac.cr/rdmcnfs/datasets /biblioteca/pdfs/nbina-9230.pdf

Soares-Filho, B. S., Moutinho, P., Nepstad, D., Anderson, A., Rodrigues, H., Garcia, R. … Maretti, C. (2010). Role of Brazilian Amazon protected areas in climate change mitigation. Proceedings of the National Academy of Sciences of the United States of America (PNAS), 107(24), 10821-10826. doi: 10.1073/pnas.0913048107

Steinfeld, H. (2002). Ganadería y medio ambiente: beneficios económicos y ambientales: producción animal y el medio ambiente en Centroamérica. San José: FAO.

Stocking, M. y Murnaghan, N. (2003). Manual para la evaluación de campo de la degradación de la tierra. Madrid: S. A. Mundi-Prensa Libros.

Szott, L; Ibrahim, M., & Beer, J. (2000). The hamburger connection hangover: cattle pasture land degradation and alternative land use in Central America. (Informe técnico 313). Turrialba: CATIE.

Valerio, C. (1998). Anotaciones sobre Historia Natural de Costa Rica. San José: UNED.

Van Westen, C. J. (1993). Application of Geographic Information Systems to Landslide Hazard Zonation (Vol. 1, N.º 5). Enschede: ITC-Publication.

Van Westen C. J., Rengers, N., & Soeters, R. (2003). Use of Geomorphological Information in Indirect Landslide Susceptibility Assessment. Natural Hazards, 30(3), 399-419. Retrieved from https://link.springer.com/article/10.1023 /B:NHAZ.0000007097.42735.9e

Zinck, A., López, J., Metternicht, G., Shrestha, D., & Vázquez-Selem, L. (2001). Mapping and modeling mass movements and gullies in mountainous areas using remote sensing and GIS techniques. International Journal of Applied Earth Observation and Geoinformation, 3(1), 43-53. doi. 10.1016/S0303-2434(01)85020-0

Zweig, M. H., & Campbell G. (1993). Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clinical Chemistry, 39(4), 561-77. Retrieved from http://clinchem.aaccjnls.org/content/clinchem /39/4/561.full.pdf

---