| ISSN Electrónico: 2215-3470 DOI: http://dx.doi.org/10.15359/ru.33-2.4 |
UNICIENCIA Vol. 33, N° 2. Julio-Diciembre, 2019 URL: www.revistas.una.ac.cr/uniciencia Correo electrónico: revistauniciencia@una.cr |
 |
 |
Estocásticos y docencia de la educación especial: distribuciones centradas y uniformes |
Stochastics and special education teaching: centered and uniform distributions
Estocásticos e docência da educação especial: distribuições centradas e uniformes
José Marcos López-Mojica
mojicajm@gmail.com
Facultad de Matemáticas, Universidad Autónoma de Guerrero,
Acapulco, Guerrero, México.
Orcid: http://orcid.org/0000-0002-7330-9979
Recibido-Received: 19/jun/2018 ● Corregido-Corrected: 15/set/2018.
Aceptado-Accepted: 26/set/2018 ● Publicado-Published: 31/jul/2019.
|
Resumen El presente artículo forma parte de un proyecto más amplio que se interesó en señalar los procesos de enseñanza y de aprendizaje de estocásticos en la educación especial. Aquí se presenta, de manera cualitativa, lo concerniente a la docencia de este nivel educativo. La perspectiva teórica consideró tres ejes rectores: epistemológico, cognitivo y social. De las tres fases de la investigación, en parte de la segunda enfocamos la introducción de la noción de distribución de probabilidad para cuatro docentes en un escenario denominado estudio dirigido, con la instrumentación de guiones de enseñanza y de bitácora; los datos se registraron con videograbación y escritura en papel. Además, se aplicó el órgano operativo y la célula de análisis de la enseñanza. Los resultados conciernen a la adquisición, de manera gradual por parte de las docentes, de las ideas de espacio muestra, medida de probabilidad, variable aleatoria (frecuencias relativas) y distribución y simetría. Palabras clave: didáctica de la probabilidad; probabilidad; educación especial; formación docente. Abstract This article is part of a more extensive project aimed at analyzing stochastics teaching and learning processes in special education. The teaching of this educational level is presented here using a qualitative approach. From a theoretical perspective, three guiding axes were considered: the epistemological, cognitive and social axes. The larger study was divided into three phases. This paper will be focused partly on the second phase, particularly on the introduction of the probability distribution for four teachers in a guided study scenario, using teaching scripts and logbooks as instruments. Data was recorded in video and in writing. In addition, operational body and teaching analysis unit were applied. Results include the teachers’ gradual acquisition of the ideas of sample space, probability measure, random variable (relative frequencies), distribution, and symmetry. Keywords: didactics of probability; probability; special education; teacher training. Resumo Este artigo é parte de um projeto mais amplo interessado em apontar os processos de ensino e aprendizagem de estocásticos na educação especial. Aqui apresentamos, qualitativamente, o que diz respeito ao ensino deste nível educacional. A perspectiva teórica considerou três eixos norteadores: epistemológico, cognitivo e social. Das três fases da pesquisa, parte da segunda enfocamos a introdução de como a probabilidade é distribuída para quatro docentes em um cenário denominado estudo dirigido, com a instrumentação de roteiros de ensino e de diário; os dados foram registrados com gravação de vídeo e escrita em papel. Além disso, foram aplicados o órgão operacional e a célula de análise de ensino. Os resultados dizem respeito à aquisição gradual por parte dos docentes das ideias de espaço amostral, medida de probabilidade, variável aleatória (frequências relativas) e distribuição e simetria. Palavras-chave: didática da probabilidade; probabilidade; educação especial; formação de docentes |
En el nivel internacional, cada vez es más notoria la preocupación por identificar, desde la matemática educativa, los requerimientos necesarios para la atención de personas con necesidades educativas especiales (NEE), asociadas o no a una discapacidad, y así ofrecer una educación matemática básica integral.
Por ejemplo, Soares y Sales (2018) recuperan investigaciones realizadas en Brasil sobre la educación matemática de la población sorda. Presentan una tendencia hacia la cual se dirigen las pesquisas en ese país. Establecen cuatro categorías: formación de profesores, adaptaciones curriculares, educación matemática y comunicación, y enseñanza y aprendizaje. Concluyen la importancia y dificultad de la inclusión del estudiante sordo al nivel medio que permita desarrollar competencias y así garantizar su ingreso a una etapa superior, pues el estudiante debe someterse a las condiciones institucionales y a la práctica oralista del docente, lo que compromete su aprendizaje.
Por su lado, Bruno y Noda (2010) presentan parte de un informe sobre las investigaciones en educación matemática que se interesan por las necesidades educativas especiales. Resulta que el área de las matemáticas más estudiada es aquella sobre el número y sus operaciones (adición y sustracción) de uno o dos dígitos. Esta se centra en el nivel primario y escasea en una etapa infantil, secundaria y universitaria; o bien se refiere a otros ámbitos de las matemáticas como geometría, álgebra, cálculo, probabilidad o estadística. Las autoras señalan la necesidad de atender la formación del docente que trabaja con los alumnos con NEE y de estrategias que favorezcan una adquisición de los conceptos matemáticos por parte de los estudiantes.
Al respecto, Bolaños, Céspedes y González (2016) establecen la importancia de indagar sobre las experiencias docentes de matemáticas que han favorecido la inclusión de estudiantes invidentes en el nivel superior. Concluyen imperante la preparación de los profesores de este nivel educativo y área, en el tratamiento de las NEE asociadas a una discapacidad y la escasa infraestructura que limita la integración de los alumnos.
Aké (2016) reflexiona sobre los retos a los que se enfrentan profesores de matemáticas y de educación especial. Para los primeros, una dificultad es promover aprendizajes específicos de esta ciencia en personas con NEE. En los segundos, una complicación es introducirse al aprendizaje de las matemáticas cuando presentan una escasa formación en esta disciplina y una desvinculación con su pensamiento matemático.
Como se podrá notar, la práctica del docente es un factor fundamental en la enseñanza de los tópicos matemáticos a personas con discapacidad, por lo que su preparación en estrategias que consideren las características de la población y en el contenido matemático es sustancial. Lo anterior toma relevancia cuando las docentes son del área de educación especial y en sus aulas interactúan una diversidad de discapacidades.
En ese sentido, es relevante investigar sobre la comprensión de estocásticos de docentes en servicio de la educación especial. Por un lado, desarrollar un pensamiento probabilístico impone un modo distinto de pensar (Fischbein, 1975), porque el pensamiento se abre a lo posible (Piaget, 1982) y, en consecuencia, al desarrollo de un pensamiento crítico. Además, los temas de estocásticos convocan la promoción de otros conceptos matemáticos (Steinbring, 2005) y permiten dotarle de otro sentido por su uso. También con los estocásticos se puede establecer una red conceptual para la constitución del pensamiento matemático.
Tratar los temas de probabilidad con los docentes del nivel educativo en cuestión permitiría que estos los incluyan en la formación matemática de los niños y así les ofrezcan un acceso al estudio de fenómenos aleatorios de manera sistemática. Es decir, se estaría preparando a los alumnos a enfrentarse a situaciones tanto deterministas como indeterministas y se garantiza, de cierta manera, una educación matemática básica integral.
Por lo tanto, el presente informe concierne a una investigación que se desarrolló en el contexto de la educación especial, por lo que interesó lo que institucionalmente se plantea para esta modalidad educativa: los servicios que ofrece, los planes y programas de estudio que la rigen, los libros de texto y la formación docente que prescribe.
Analizar el desempeño de docentes en un estudio dirigido (Ojeda, 2006) a estocásticos para la educación especial, como una forma de actualización enfocada en introducir nociones de probabilidad en el aula, permite establecer un marco de referencia para su tratamiento en el nivel educativo en cuestión. Se parte de la idea de que no se pueden enseñar conceptos matemáticos si no se conocen. Por lo tanto, es importante que los docentes se enfrenten a las situaciones matemáticas antes de tratarlas en el aula con los niños, en este caso, a situaciones aleatorias. De manera particular, interesa la distribución de probabilidades, medida de probabilidad, espacio muestra y variable aleatoria, pues constituyen una valiosa fuente en la formación matemática por las redes implicadas en su desarrollo.
Un primer acercamiento al estudio de las distribuciones centradas y uniformes se presenta en Piaget e Inhelder (1951). Con el objetivo de investigar sobre el origen de la idea de azar, los autores propusieron una situación aleatoria que implica el acomodo de canicas en bandejas. Interesó el mecanismo de la distribución de estas, al señalar la simetría de las trayectorias y, de manera gradual, pasaron de distribuciones centradas a sesgadas. Según los autores, lo anterior desembocaría en la distribución normal.
Tauber (2001) señala que la distribución normal es una pieza clave en la estadística. Según la autora, con ella se pueden estudiar fenómenos de tipo físicos, biológicos, psicológicos, sociológicos o aquellos cuya distribución sea simétrica. Es importante, dado que con tal mecanismo se pueden tomar decisiones. Es de notar que a las docentes de educación especial no se les trató matemáticamente la distribución normal, pero sí actividades para desarrollar nociones y que implicarían una mejor introducción a los niños.
Cabe señalar que en México la educación especial es una modalidad educativa destinada a ofrecer servicios a personas que presentan necesidades educativas especiales asociadas o no a una discapacidad (Secretaría de Educación Pública, 2004), ya sea integradas en escuelas regulares (Servicios de Apoyo a la Educación Regular –USAER–) o espacios exclusivos para ellas, cuando no se pueden integrar a las escuelas regulares (Centro de Atención Múltiple –CAM–).
Elementos teóricos: tres ejes rectores
La investigación consideró la articulación de tres ejes rectores (Ojeda, 1994; 2006): epistemológico, cognitivo y social, los cuales se detallan a continuación.
•Eje epistemológico. Está relacionado con el conocimiento sobre probabilidad y estadística.
•Eje cognitivo. Son de interés los procesos del individuo frente a situaciones azarosas.
•Eje social. Concierne al contexto de la educación especial y las interacciones entre los docentes, cuando el conocimiento matemático es objeto de enseñanza.
El eje epistemológico toma la propuesta de Heitele (1975) sobre diez ideas fundamentales de estocásticos como guía para un currículum en espiral. Argumenta que una idea fundamental es aquella que proporciona al individuo modelos explicativos tan eficientes como sea posible. Para efectos del documento, se consideran: espacio muestra, medida de probabilidad, variable aleatoria, distribución y simetría, independencia, muestra. También es de interés la constitución de la idea de azar en el individuo, según Piaget e Inhelder (1951). La conclusión es que la idea de azar no es innata, sino que se constituye gradualmente, en correspondencia con la adquisición de las operaciones reversibles. Para las distribuciones centradas y uniformes, la situación consiste en el acomodo azaroso de canicas, liberadas por los embudos, en las casillas de la parte inferior de las bandejas (véase la Figura 1). De manera gradual por el número de casillas en las bandejas, se pasa de la distribución uniforme (bandeja I) a la centrada (bandejas II, III y IV) y a la sesgada (bandeja V).
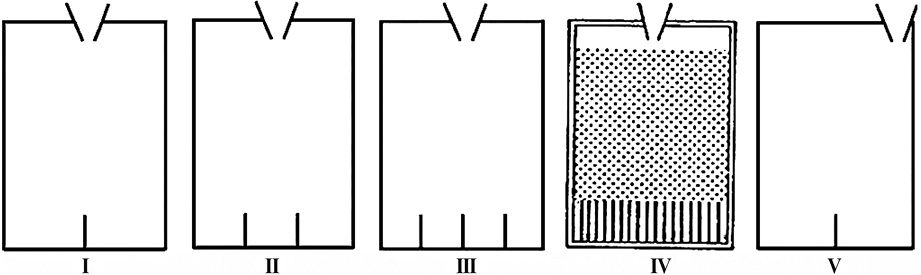
Figura 1. Esquemas de las bandejas para distribuciones
Extraído de: La Génèse de l´idée de Hasard Chez l´enfant, p. 28, por J. Piaget y B. Inhelder, 1951. PUF, París.
Para la adquisición de las distribuciones, se establecen estadios: el de operaciones preconcretas se caracteriza por la ausencia de una distribución del todo; en operaciones concretas el individuo inicia con una comprensión general de la distribución del todo; las operaciones formales sobresalen por cuantificar de la distribución del todo (Piaget e Inhelder, 1951).
En el eje cognitivo, fue de interés la intuición (Fischbein, 1975), que se caracteriza como un programa de acción parcialmente autónomo en la cognición y que es una síntesis de la experiencia individual en un dominio dado, no es susceptible de análisis, es inmediata. Particularmente, la intuición de frecuencia relativa (Fischbein, 1975) se desarrolla naturalmente “como consecuencia del hecho de que el individuo vive en un entorno caracterizado por fenómenos estocásticos” (Fischbein, 1975, p. 58). Esta intuición, mediante experimentos de aprendizaje probabilístico, mejora con la edad. Si la intuición se observa como un resultado cognitivamente fijado de experiencias acumulables, parece razonable que la intuición de frecuencia relativa se desarrolle de un modo natural como resultado de las experiencias del individuo con situaciones que implican sucesos aleatorios. Por tanto, es un conocimiento que se deriva de la experiencia.
El eje social toma en consideración la propuesta del triángulo relacional (véase la Figura 2), para explicar la naturaleza epistemológica de la apropiación de un concepto matemático (Steinbring, 2005) y su significado socialmente constituido.
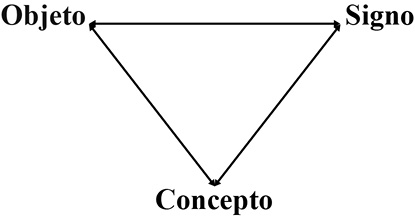
Figura 2. Triángulo epistemológico para la constitución del concepto matemático
Extraído de: The construction of new mathematical knowledge in classroom interaction, p. 22, por H. Steinbring, 2005. Springer, USA.
La constitución del concepto matemático resulta de la interacción entre él, el objeto y el signo, de modo que el primero siempre es perfectible y se distingue de, y entre, objeto y signo (Steinbring, 1991; Ojeda, 2006). El triángulo epistemológico es una relación funcional para la constitución del conocimiento, formado por tres componentes: objeto, aquello que es producto de la actividad intelectual del sujeto; signo, la representación de esa abstracción; concepto, lo que apela a la descripción específica de ese objeto y va desde nociones, a ideas, a conceptos en interrelación constante con el objeto y el signo.
Procedimiento de la investigación
La investigación se ajustó a los lineamientos del órgano operativo y a los de la célula de análisis de la enseñanza (Ojeda, 2006). El órgano establece condiciones para el arribo de la investigación al aula; además, indica cómo caracterizar los procesos de enseñanza por los elementos conceptuales implicados en las experiencias que tienen lugar en ese espacio, los cuales se identifican mediante un análisis, cuyos resultados se van integrando a la investigación y permiten, a la vez, la autocrítica para el investigador y el docente titular.
En la conformación del órgano operativo se encuentra el espacio denominado estudio dirigido (Ojeda, 2006) a estocásticos para la docencia de educación especial. Aquí se comparten experiencias de enseñanza y de investigación; es decir, interactúan las docentes titulares y los investigadores. Se perfilan en conjunto las estrategias y acciones específicas por desarrollar en la enseñanza de la probabilidad en las aulas, según las necesidades de la investigación. Se analizan las actividades antes de su implementación en sus aulas.
Por su parte, la célula de análisis para la enseñanza “pone en juego, para cada escenario, elementos teóricos y aspectos hacia los cuales se ha dirigido el estudio” (Ojeda, 2006, p. 203). La célula organiza los elementos provenientes del eje epistemológico, del cognitivo y del social, de modo tal que ella permite esquematizar y contextualizar el proceso de enseñanza e indica la forma de someterlo a escrutinio. La investigación consideró criterios de análisis de los datos recopilados, los cuales se describen seguidamente.
•Situación: este término hace referencia a la relación del individuo con su medio ambiente, el cual condiciona, limita, funda y determina posibilidades (Abbagnano, 1974).
•Ideas fundamentales de estocásticos: medida de probabilidad, espacio muestra, regla de la adición, regla del producto e independencia, equidistribución y simetría, combinatoria, modelo de urna y simulación, variable aleatoria, ley de los grandes números y muestra (Heitele, 1975).
•Otros conceptos matemáticos: números naturales y el cero, su orden, operaciones aritméticas básicas, razón y proporción, producto cartesiano, por mencionar algunos.
•Recursos semióticos: gráficas, figuras, diagramas, notación matemática, lengua natural escrita. Ojeda (2006) argumenta que se hace referencia a “recursos semióticos” en lugar de “representaciones semióticas”, ya que esta última frase corresponde a una interiorización de los usos de esos recursos, que no es inmediata a su presentación.
•Términos empleados: las palabras y las frases que aluden a estocásticos, ya sea técnicas o cotidianas (Ojeda, 2006).
La investigación se organizó en tres fases; para el presente documento, se muestra, en parte de la segunda fase, lo concerniente a la comprensión de los estocásticos de las docentes titulares en el espacio de estudio dirigido. En este espacio se aplicó a las docentes la actividad de enseñanza, conducida por los investigadores, para identificar las relaciones establecidas entre el docente y el concepto matemático. Las docentes participantes fueron R (primer grado), JH (tercer grado), M (cuarto grado) y S (sexto grado), todas ellas psicólogas de formación y con 15 años, en promedio, de experiencia en la educación especial; atendían en sus grupos a una heterogeneidad de discapacidades. Por lo anterior, se podría tener síndrome de Down, trastorno del espectro autista, discapacidad intelectual, por mercionar algunos casos.
Se utilizaron los métodos de la bitácora y de la experienciación (Maturana, 2003), así como se aplicaron los instrumentos de recolección de datos, que son los guiones de plan de clase y las hojas de control; las técnicas de registro fueron la escritura con lápiz y papel, o en pizarrón, la videograbación y su transcripción.
La actividad de referencia fue “distribuciones centradas y uniformes”. El objetivo fue introducir la idea de azar en el acomodo azaroso de las canicas, además de otros conceptos matemáticos como cantidad y proporción. Consistió en bandejas rectangulares (véase la Figura 3), similares a las propuestas por Piaget e Inhelder (1951), con embudos en la parte superior y casillas igualmente distribuidas en la inferior. Se liberan, por los embudos, canicas del mismo tamaño y color, las cuales se distribuyen al azar en las casillas. Se utilizaron 40 canicas para las bandejas I y V; 60, para las bandejas II y III; 200, para la bandeja IV. A las docentes se les pedía una anticipación, en dibujo, del acomodo de las canicas, antes de vaciarlas por los embudos. Su producción se comparaba con lo que resultaba de manera efectiva en las bandejas, para plantear cuestiones sobre lo azaroso de la situación.

Figura 3. Bandejas de madera para “distribuciones centradas y uniformes”
Elaboración propia del estudio.
El fenómeno aleatorio en foco en cada caso es el acomodo azaroso de las canicas en las casillas, después de su vaciado por los embudos. El espacio muestra son las posibles casillas en las que pueden caer las canicas. La medida de probabilidad se considera, cualitativamente, con la relación del número de posibilidades de que una canica caiga en una casilla respecto al número total de posibilidades de ocupación de las casillas posibles. De manera cualitativa, con la asignación numérica del total de canicas ocupadas en cada casilla se trata la variable aleatoria; es decir, la frecuencia relativa de una casilla es el número de sus canicas ocupantes respecto al total de canicas liberadas por el embudo. Se apela a la ley de los grandes números con la forma de la distribución de un número grande de canicas después de su vaciado. Gradualmente, por el número de casillas en las bandejas, se pasó de una distribución uniforme (bandeja I) a distribuciones centradas (bandejas II, III y IV) y a una sesgada (bandeja V). En la siguiente Tabla 1, se presenta el resultado de la aplicación de los criterios de análisis a la actividad.
Tabla 1
Caracterización de la actividad “distribuciones centradas y uniformes”
|
Situación |
Ideas fundamentales de estocásticos |
Otros conceptos matemáticos |
Recursos semióticos |
Términos para referirse a estocásticos |
|
Distribución aleatoria de canicas en casillas |
Espacio muestra, medida de probabilidad, variable aleatoria, ley de los grandes números |
Números naturales, proporción |
Figuras, lengua natural escrita |
Queda, acomodan, distribuyen, curva, caen, chocan, más fácil que |
Nota: Fuente propia de la investigación.
Comprensión de estocásticos de las docentes
Como se adelantó, la actividad se aplicó en el espacio de estudio dirigido a estocásticos para la educación especial, se examinó el desempeño de las docentes respecto a las ideas fundamentales, a los otros conceptos matemáticos requeridos para responder las preguntas planteadas en la actividad, a los recursos semióticos utilizados en sus argumentaciones y tanto a los términos como a las expresiones utilizados referidos a los conceptos de probabilidad y de estadística.
Gradualmente, las docentes identificaron las distribuciones aleatorias centradas y la uniforme; la advertencia de la distribución sesgada no revistió una dificultad para ellas; además, de manera cualitativa, asignaron probabilidades a las casillas de las bandejas después de la bandeja II.
En las transcripciones de los episodios que citamos, las iniciales corresponden al nombre de las docentes titulares [JH, M, R, S], a todas [T] y a los investigadores [I].
Medida de probabilidad. Ante la petición de lo predicho en cuanto a la distribución de las canicas antes del vaciado, las docentes asignaron probabilidades a las casillas de las bandejas. En un principio, para la bandeja I (dos casillas), a pesar de que identificaron que en ambas casillas era posible que cayeran las canicas, las docentes mostraron confusión al asignar la probabilidad, salvo M, que la asignó correctamente.
|
I: |
… a ver, profesoras, si lanzamos las canicas, ¿dónde quedarán? Tenemos que dibujar en el esquema cómo quedarán las canicas al alimentar la bandeja. |
|
JH: |
Aquí [señala la casilla derecha de la bandeja I]. |
|
I: |
¿Sí? |
|
M: |
Cuando caen las canicas, chocan en el muro; entonces, tenemos dos opciones, unas se van por el lado derecho y otras por el lado izquierdo. |
|
I: |
¿En cuál de las dos casillas es más fácil que queden las canicas? |
|
M, S: |
En las dos. |
|
I: |
Si les pregunto: ¿cuál es la probabilidad de que una canica, al ser lanzada [liberada], caiga en una de las casillas? |
|
JH: |
Dos de una, ¿no? |
|
M: |
¡No! Una de dos. |
|
S: |
Dos de una, porque son dos lugares para una canica. |
|
M: |
Una de dos. |
|
T: |
[Semblante de confusión]. |
|
I: |
Una de dos. Si la canica cae aquí [señala la casilla derecha] ocupa una casilla de dos, o si cae acá, lo mismo. Entonces ¿cuál sería la probabilidad? |
|
M, S: |
50 %. |
|
JH: |
Una de dos. |
Docentes JH y S invirtieron la relación entre los casos favorables con el total de casos posibles, expresaron dos de una en lugar de una de dos. Docentes M y S, a pesar de asignar en un principio la probabilidad a manera de fracción, respondieron al final con porcentajes. Lo anterior evocó al enfoque frecuencial de la probabilidad más que al clásico.
Con la bandeja II (tres casillas), docentes M, JH y S reconocieron que una canica podía ocupar una de las tres casillas. Cuando se les preguntó cuál probabilidad asignarían a que una canica ocupara una de las casillas, respondieron “una de tres”. Docentes M y S asignaron a cada casilla una probabilidad de “33 %”, a pesar de anticipar mayor ocupación de canicas para la casilla central.
|
I: |
… ahora para esta bandeja [tres casillas], si vaciamos las canicas, ¿de qué manera van a quedar acá [señala la parte inferior de las bandejas]? |
|
S: |
Yo siento que el de acá va a estar difícil que se llene [señala la casilla del lado derecho]. |
|
I: |
¿Por qué? |
|
S: |
No sé. |
|
I: |
Entonces, ¿usted tiene la idea de que siempre van a caer ahí, [de que] se van a cargar hacia acá [señala la casilla de la derecha]? |
|
S: |
Sí. |
|
I: |
¿Todas? |
|
S: |
¡No!, algunas. |
|
I: |
Si yo les pregunto: ¿cuál es la probabilidad de que alguna canica… al liberar la canica tome una de estas casillas? |
|
JH: |
Una de tres, ya le entendí. Sí, porque el objeto [se refiere a la canica] va a ser uno pero hay tres casillas. |
|
M: |
Como un 33 %, ¿no? |
|
S: |
[Afirma con la cabeza] Como un 33 %. |
De igual manera, en el caso de la bandeja III (cuatro casillas), las docentes asignaron la probabilidad “1/4” a que una canica ocupara una de las casillas, sin advertir que las casillas centrales tenían mayor probabilidad que las laterales, hasta la intervención de uno de los investigadores.
|
I2: |
… Por ejemplo, en la bandeja de tres casillas, dijeron 33 %, pero se acumularon más al centro… |
|
T: |
Sí. |
|
I2: |
Entonces, si uno ve, el total debe ser el 100 % de posibilidades. Entonces uno puede decir 25 % de este lado, el izquierdo, 25 % en el derecho y 50 % en el medio [casillas centrales]. |
|
S: |
Para que todo sea 100 %. |
|
T: |
¡Ah! |
|
I2: |
¿Sí? Por eso la tendencia a la montañita. |
|
M: |
Entonces sería 40, 40 [indica las casillas centrales], 80 y diez y diez [señala las casillas laterales]. |
Como se puede notar, docente M, identificó, de manera inmediata, que la suma de los porcentajes asignados correspondía al total de las posibilidades, por tanto, ella propone porcentajes a las casillas de la bandeja, de modo que las centrales tienen 40 % y las laterales 10 % (Figura 4).
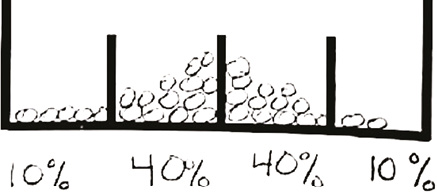
Figura 4. Asignación de probabilidades a las casillas por Docente M
Elaboración propia del estudio.
Para las demás bandejas, docentes M y S advirtieron que era más probable que en las casillas centrales se concentraran más canicas; las probabilidades asignadas por docente M a las casillas de la bandeja IV quedaron distribuidas de la siguiente manera: 5 %, 10 %, 15 %, 40 %, 15 %, 10 %, 5 %; como se puede notar identificó la simetría en la distribución. Para el caso de la bandeja V, distribución sesgada, previeron y estimaron las probabilidades sin dificultad; por ejemplo, docente JH propuso 40 %, 60 %.
Espacio muestra. Para esta idea fundamental, las docentes identificaron gradualmente las casillas en las que podrían caer las canicas. En la bandeja I, por ejemplo, ellas se percataron de que las canicas podían caer en una de las dos casillas.
|
I: |
… a ver, profesoras, si lanzamos las canicas, ¿dónde quedarán? Tenemos que dibujar en el esquema cómo quedarán las canicas al alimentar la bandeja. |
|
JH: |
Aquí [señala el lado derecho de la bandeja I]. |
|
I: |
¿Sí? |
|
M: |
Cuando caen las canicas, chocan en el muro; entonces, tenemos dos opciones, unas se van por el lado derecho y otras por el lado izquierdo. |
|
I: |
¿En cuál de las dos casillas es más fácil que queden las canicas? |
|
M, S: |
En las dos. |
Para la bandeja IV, las docentes identificaron que las canicas podían seguir una variedad de trayectorias antes de llegar a una de las casillas; una de ellas [docente S] se levantó hacia donde estaba el tablero de madera y comenzó a señalar algunas posibles trayectorias que una canica pudiera recorrer.
Variable aleatoria. Para esta idea fundamental, se hizo referencia, cualitativamente, a la relación del número de canicas ocupantes de cada casilla, respecto al total de canicas liberadas por el embudo. Las docentes, en sus dibujos, distribuyeron las canicas en cada una de las casillas (Figura 5).
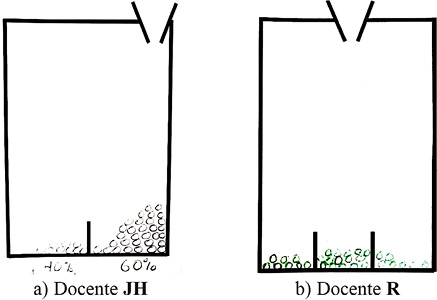
Figura 5. Distribución y asignación de canicas según las docentes JH y R
Elaboración propia del estudio.
Ley de los grandes números. Esta idea fundamental se trató en la actividad, de manera cualitativa, con la distribución de 200 canicas en las 14 casillas de la bandeja IV. Las docentes asignaron mayor probabilidad a las casillas centrales y menor probabilidad a las de los extremos. Según los dibujos de las participantes, hubo una aproximación a la distribución acampanada; por ejemplo, docente R dibujó más canicas en las centrales y menos en los extremos (ver Figura 6).

Figura 6. Distribución de “muchas” canicas por parte de docente R
Elaboración propia del estudio.
Proporción. La actividad, con foco en las ideas fundamentales de estocásticos, requirió otros conceptos matemáticos a los que las docentes les darían sentido, al aplicarlos a situaciones aleatorias y no solo deterministas; fue el caso de la proporción. Las docentes, de manera cualitativa, estimaban la probabilidad de que las canicas cayeran en una u otra de las casillas de las bandejas, por medio de porcentajes. En un momento, ellas reconocieron que la suma de los porcentajes de canicas en las distintas celdas equivaldría al 100 %; por tanto, tenían que distribuirlas en proporciones menores al 100 % en las casillas.
Recursos semióticos. Las hojas de control se diseñaron de manera tal que las figuras, imágenes o tablas eran similares al material concreto empleado, en este caso, se recurrió a esquemas de las bandejas. Los trazos de las docentes, solicitados por los investigadores, fueron un medio de que expresaran sus respuestas y revelaran algunos sesgos a las ideas de azar y de probabilidad, como el de equiprobabilidad o de una distribución centrada; pero también la aceptación de la distribución sesgada.
Enseñanza en el aula alterna. Después del desarrollo de la actividad en estudio dirigido, esta se implementó en las aulas de las docentes titulares junto con el investigador. En conjunto, establecieron alternativas de enseñanza, en consideración a las características de los alumnos con discapacidad. A ese espacio se le denominó aula alterna, por ser una alternativa a la enseñanza tradicional. Por cuestiones de espacio, solo se menciona que las docentes comenzaron a introducir las nociones de espacio muestra, frecuencia relativa, variable aleatoria a los niños con discapacidad.
Conclusiones y comentarios
Derivada de la actividad de enseñanza, las docentes iniciaron una introducción a las ideas de espacio muestra, distribución de probabilidades y de azar. Comenzaron con la identificación de las posibles canicas que tenía cada una de las bandejas; asignaron probabilidades en función de las posibilidades de las casillas de las bandejas; señalaron las posibles trayectorias que tenía una canica de recorrer en la bandeja IV.
También se pudo identificar la evolución del enfoque clásico de la probabilidad hacia el enfoque frecuencial. Las docentes, en principio, establecieron la relación entre el número de casillas que pudiera ocupar una canica con todas las posibles y emitieron expresiones como “una de las dos casillas”. Con la intervención de los investigadores, se reflexionó hacia el número de canicas que pudieran ocupar las casillas y así asignaron la probabilidad en porcentaje. Como lo señaló Fischbein (1975), la exposición a situaciones concretas que revisten una acumulación de experiencias provoca en el individuo, de manera natural, la intuición de frecuencia relativa.
Se tuvo una aproximación a la distribución normal de la probabilidad, cuando en sus dibujos asignaron más probabilidad a las casillas centrales y menos a las casillas de los extremos para la bandeja IV; además, se identificó la simetría de esta: 5 %, 10 %, 15 %, 40 %, 15 %, 10 %, 5 %.
El tipo de producción y el desempeño de las participantes sugieren la constitución de la probabilidad frecuencial. En el nivel de objeto, interesó la distribución aleatoria de las canicas, después de su vaciado en las bandejas; en el nivel de signo, la advertencia de que las posiciones finales anticipadas de las canicas correspondían a uno de muchos acomodos posibles, de manera que se fueron introduciendo nociones de espacio muestra (lo posible) y, cualitativamente, de medida de probabilidad (Steinbring, 2005).
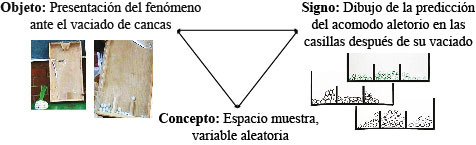
Figura 7. Triángulo epistemológico en estudio dirigido para distribuciones centradas
Elaboración propia del estudio.
Por otra parte, es necesario presentar a las docentes una diversidad de situaciones para que, de modo progresivo, otorguen mayor sentido a la idea de azar. De esa manera, podrían acercar también a los niños a los conceptos implicados. Es importante que, antes de aplicar las actividades en el aula, las docentes tengan el contacto efectivo con el fenómeno aleatorio, pues, debido a su experiencia, pueden anticipar las dificultades de los alumnos, al presentárselas en el aula, e informar sobre el tipo de adaptaciones pertinentes para desarrollar un conocimiento matemático.
Referencias bibliográficas
Abbagnano, N. (1974). Diccionario de filosofía (1.ª ed). México: Fondo de Cultura Económica.
Aké, L. P. (2016). Matemática Educativa y Educación Especial: realidades y desafíos en la formación de profesores. En J. López-Mojica y J. Cuevas (Coords.), Educación Especial y Matemática Educativa. Una aproximación desde la formación docente y procesos de enseñanza (pp. 15-32). México: CENEJUS.
Bolaños, H.; Céspedes, M. y González, C. (2016). Las experiencias del personal docente de matemática en el trabajo de aula con la población no vidente. Revista Uniciencia, 30(1), 99-114. Doi: http://dx.doi.org/10.15359/ru.30-1.6
Bruno, A. y Noda, A. (2010). Necesidades educativas especiales en matemáticas. El caso de personas con síndrome de Down. En M. Moreno, A. Estrada y J. Carrillo (Eds.), Investigación en Educación Matemática XIV (pp. 141-162). Lleida: SEIEM.
Fischbein, E. (1975). The intuitive sources of probabilistic thinking in children. Holanda: Reidel. Doi https://doi.org/10.1007/978-94-010-1858-6
Heitele, D. (1975). An epistemological view on fundamental stochastic Ideas. Educational Studies in Mathematics, 6(2), 187-205. Doi: https://doi.org/10.1007/BF00302543
Maturana, H. (2003). Desde la Biología a la Psicología. Argentina: Lumen.
Ojeda, A. M. (1994). Understanding fundamental ideas of probability at pre-university levels. (Tesis doctoral). King’s College London, UK.
Ojeda, A. M. (2006). Estrategia para un perfil nuevo de docencia: un ensayo en la enseñanza de estocásticos. En E. Filloy (Ed.), Matemática Educativa, treinta años (195-215). México: Santillana-Cinvestav.
Piaget, J. (1982). Le possible et le nécéssaire. Francia: PUF.
Piaget, J. e Inhelder, B. (1951). La Génèse de l´idée de Hasard Chez l´enfant. París: PUF.
Secretaría de Educación Pública (2004). Licenciatura en Educación Especial. Programa para la transformación y el fortalecimiento académicos de las escuelas normales. Plan de estudios. México: SEP.
Soares, M. y Sales, E. (2018). Uma reflexão sobre pesquisas em Educação Matemática e Educação de Surdos. Educação Matemática Debate, 2(4), 31-56. Doi: https://doi.org/10.24116/emd25266136v2n42018a02
Steinbring, H. (1991). The concept of chance in everyday teaching: aspects of a social epistemology of mathematical knowledge. Educational Studies in Mathematics, 22, 503-522. Doi: https://doi.org/10.1007/BF00312713
Steinbring, H. (2005). The construction of new mathematical knowledge in classroom interaction. USA: Springer.
Tauber, L. (2001). La construcción del significado de la distribución normal a partir de actividades de análisis de datos. (Tesis doctoral). Facultad de Educación, Universidad de Granada, España.
Estocásticos y docencia de la educación especial: distribuciones centradas y uniformes (José Marcos López-Mojica) por Revista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported licence.
